
【题目】某高校调查喜欢“统计”课程是否与性别有关,随机抽取了55个学生,得到统计数据如表:
喜欢 | 不喜欢 | 总计 | |
男生 | 20 | ||
女生 | 20 | ||
总计 | 30 | 55 |
(1)完成表格的数据;
(2)判断是否在犯错误的概率不超过0.005的前提下认为喜欢“统计”课程与性别有关?
参考公式:![]()
| 0.025 | 0.01 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)见解析;(2)在犯错误的概率不超过0.005的前提下认为喜欢“统计”课程与性别有关.
【解析】
(1)根据表中的数据即可完成列联表;
(2)根据列联表,求出观测值,利用观测值同临界值表进行比较,即可判断.
(1)解:由表知,喜欢“统计”课程女生人数为![]() (人),
(人),
不喜欢“统计”课程的总人数为![]() (人),
(人),
不喜欢“统计”课程男生人数为![]() (人),则列联表为
(人),则列联表为
喜欢 | 不喜欢 | 总计 | |
男生 | 20 | 5 | 25 |
女生 | 10 | 20 | 30 |
总计 | 30 | 25 | 55 |
(2)解:设![]() 喜欢“统计”课程与性别无关,由(1)可知列联表为:
喜欢“统计”课程与性别无关,由(1)可知列联表为:
喜欢 | 不喜欢 | 总计 | |
男生 | 20 | 5 | 25 |
女生 | 10 | 20 | 30 |
总计 | 30 | 25 | 55 |
则![]() ,
,
所以在犯错误的概率不超过0.005的前提下认为喜欢“统计”课程与性别有关.


科目:高中数学 来源: 题型:
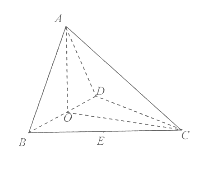
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,![]() ,
,![]() .
.
(1)求证:![]() 平面BCD;
平面BCD;
(2)求异面直线AB与CD所成角的余弦值;
(3)求点E到平面ACD的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
分组 | 频数 | 频率 | |
一组 | 0≤t<5 | 0 | 0 |
二组 | 5≤t<10 | 10 | 0.10 |
三组 | 10≤t<15 | 10 | ② |
四组 | 15≤t<20 | ① | 0.50 |
五组 | 20≤t≤25 | 30 | 0.30 |
合计 | 100 | 1.00 |

解答下列问题:
(1)这次抽样的样本容量是多少?
(2)在表中填写出缺失的数据并补全频率分布直方图;
(3)旅客购票用时的平均数可能落在哪一组?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
储蓄存款 | 5 | 6 | 7 | 8 | 10 |
(Ⅰ)求y关于t的回归方程![]()
(Ⅱ)用所求回归方程预测该地区2015年(![]() )的人民币储蓄存款.
)的人民币储蓄存款.
附:回归方程![]() 中
中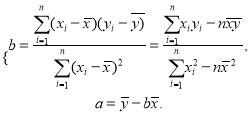
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凸![]() 边形
边形![]() 玫瑰园的
玫瑰园的![]() 个顶点各栽有1棵红玫瑰,每两棵红玫瑰之间都有一条直小路想通,这些直小路没有出现“三线共点”的情况——它们把花园分割成许多不重叠的区域(三角形、四边形、……),每块区域都栽有一棵白玫瑰(或黑玫瑰).
个顶点各栽有1棵红玫瑰,每两棵红玫瑰之间都有一条直小路想通,这些直小路没有出现“三线共点”的情况——它们把花园分割成许多不重叠的区域(三角形、四边形、……),每块区域都栽有一棵白玫瑰(或黑玫瑰).
(1)求出玫瑰园里玫瑰总棵树![]() 的表达式.
的表达式.
(2)花园里能否恰有99棵玫瑰?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.且曲线
轴的正半轴为极轴建立极坐标系.且曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为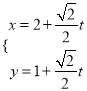 (
(![]() 为参数),圆
为参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com