
【题目】我们称n(![]() )元有序实数组(
)元有序实数组(![]() ,
,![]() ,…,
,…,![]() )为n维向量,
)为n维向量,![]() 为该向量的范数.已知n维向量
为该向量的范数.已知n维向量![]() ,其中
,其中![]() ,
,![]() ,2,…,n.记范数为奇数的n维向量
,2,…,n.记范数为奇数的n维向量![]() 的个数为
的个数为![]() ,这
,这![]() 个向量的范数之和为
个向量的范数之和为![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)当n为偶数时,求![]() ,
,![]() (用n表示).
(用n表示).
【答案】(1)![]() ,
,![]() .(2)
.(2)![]() ,
,![]()
【解析】
(1)利用枚举法将范数为奇数的二元有序实数对都写出来,再做和;(2)用组合数表示![]() 和
和![]() ,再由公式
,再由公式![]() 或
或![]() 将组合数进行化简,得出最终结果.
将组合数进行化简,得出最终结果.
解:(1)范数为奇数的二元有序实数对有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
它们的范数依次为1,1,1,1,故![]() ,
,![]() .
.
(2)当n为偶数时,在向量![]() 的n个坐标中,要使得范数为奇数,则0的个数一定是奇数,所以可按照含0个数为:1,3,…,
的n个坐标中,要使得范数为奇数,则0的个数一定是奇数,所以可按照含0个数为:1,3,…,![]() 进行讨论:
进行讨论:![]() 的n个坐标中含1个0,其余坐标为1或
的n个坐标中含1个0,其余坐标为1或![]() ,共有
,共有![]() 个,每个
个,每个![]() 的范数为
的范数为![]() ;
;
![]() 的n个坐标中含3个0,其余坐标为1或
的n个坐标中含3个0,其余坐标为1或![]() ,共有
,共有![]() 个,每个
个,每个![]() 的范数为
的范数为![]() ;
;
![]() 的n个坐标中含
的n个坐标中含![]() 个0,其余坐标为1或
个0,其余坐标为1或![]() ,
,
共有![]() 个,每个
个,每个![]() 的范数为1;所以
的范数为1;所以
![]() ,
,
![]() .
.
因为![]() ,①
,①
![]() ,②
,②
![]() 得,
得,![]() ,
,
所以![]() .
.
解法1:因为![]() ,
,
所以![]() .
.
![]()
![]()
![]() .
.
解法2:![]() 得,
得,![]() .
.
又因为![]() ,所以
,所以
![]()
![]()
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】传染病的流行必须具备的三个基本环节是:传染源、传播途径和人群易感性.三个环节必须同时存在,方能构成传染病流行.呼吸道飞沫和密切接触传播是新冠状病毒的主要传播途径,为了有效防控新冠状病毒的流行,人们出行都应该佩戴口罩.某地区已经出现了新冠状病毒的感染病人,为了掌握该地区居民的防控意识和防控情况,用分层抽样的方法从全体居民中抽出一个容量为100的样本,统计样本中每个人出行是否会佩戴口罩的情况,得到下面列联表:
戴口罩 | 不戴口罩 | |
青年人 | 50 | 10 |
中老年人 | 20 | 20 |
(1)能否有![]() 的把握认为是否会佩戴口罩出行的行为与年龄有关?
的把握认为是否会佩戴口罩出行的行为与年龄有关?
(2)用样本估计总体,若从该地区出行不戴口罩的居民中随机抽取5人,求恰好有2人是青年人的概率.
附: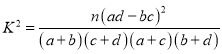
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在
在![]() 处有极值,且
处有极值,且![]() ,则称
,则称![]() 为函数
为函数![]() 的“F点”.
的“F点”.
(1)设函数![]() (
(![]() ).
).
①当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
②若函数![]() 存在“F点”,求k的值;
存在“F点”,求k的值;
(2)已知函数![]() (a,b,
(a,b,![]() ,
,![]() )存在两个不相等的“F点”
)存在两个不相等的“F点”![]() ,
,![]() ,且
,且![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥P-ABC中,平面PAB⊥平面ABC,△ABC是边长为![]() 的等边三角形,
的等边三角形,![]() ,点O,M分别是AB,BC的中点.
,点O,M分别是AB,BC的中点.
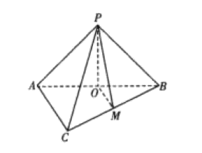
(1)证明:AC//平面POM;
(2)求点B到平面POM的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.

(1)求在未来的连续4天中,有2天的日销售量低于100枝且另外2天不低于150枝的概率;
(2)用![]() 表示在未来4天里日销售量不低于100枝的天数,求随机变量
表示在未来4天里日销售量不低于100枝的天数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,
,![]() 是椭圆上关于原点
是椭圆上关于原点![]() 对称的两个动点,当点
对称的两个动点,当点![]() 的坐标为
的坐标为![]() 时,
时,![]() 的周长恰为
的周长恰为![]() .
.
(1)求椭圆的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,且
两点,且![]()
![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com