
����Ŀ����96�죨������ȫ���Ǿ���Ʒ������2017��3��23����25�����Ĵ��ٰ�.���Ὺʼǰ��չ�ݸ���һ�Ҵ�����ɫ����Ϊ���о��λ��������������ԭ���������Ĺ�ϵ�����������5�ν���IJλ�����![]() �����ˣ����������ԭ��������
�����ˣ����������ԭ��������![]() ���������õ��������ݣ�
���������õ��������ݣ�

��������������������ݣ����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
������֪����ԭ���ϵķ���![]() ��Ԫ��������
��Ԫ��������![]() �������Ĺ�ϵΪ
�������Ĺ�ϵΪ![]() Ͷ��ʹ�õ�ÿ��ԭ������Ӧ����������Ϊ600Ԫ�������ԭ����ֻ��������.������ԭ������ǡ�����꣬��Ϥ���ν����Լ��14���˲μӣ����ݣ�������������Իع鷽�̣�Ԥ�����Ӧ������ٴ�ԭ���ϣ����ܻ�����������������Ƕ��٣���ע������
Ͷ��ʹ�õ�ÿ��ԭ������Ӧ����������Ϊ600Ԫ�������ԭ����ֻ��������.������ԭ������ǡ�����꣬��Ϥ���ν����Լ��14���˲μӣ����ݣ�������������Իع鷽�̣�Ԥ�����Ӧ������ٴ�ԭ���ϣ����ܻ�����������������Ƕ��٣���ע������![]() ��������
��������![]() ԭ���Ϸ��ã�.
ԭ���Ϸ��ã�.
���ο���ʽ�� 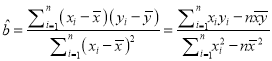 ��
�� ![]() ��
��
���𰸡���1��![]() ��2���ò���Ӧ����35��ԭ���ϣ����ܻ������������������10370Ԫ.
��2���ò���Ӧ����35��ԭ���ϣ����ܻ������������������10370Ԫ.
�����������������
(1)�����������ûع鷽��Ϊ![]() .
.
(2)���ûع鷽��Ԥ����Ҫԭ����34.2������Ϸֶκ������ۿɵøò���Ӧ����35��ԭ���ϣ����ܻ������������������10370Ԫ.
���������
���������ݣ����![]() ��
��
![]() ��
��
![]()
![]() ��
��
![]()
![]() ��
��
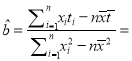
![]() ��
�� ![]()
![]() ��
��
����![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() .
.
�����ɣ�������������Իع鷽�̣���![]() ʱ��
ʱ�� ![]() ��
��
��Ԥ����Ҫԭ����34.2����
��Ϊ![]()
![]()
���ԣ���![]() ������
������![]()
![]() ��
��
��![]() ʱ������
ʱ������![]()
![]() Ԫ��
Ԫ��
��![]() ������
������![]()
![]() ��
��
��![]() ʱ������
ʱ������![]()
![]() Ԫ��
Ԫ��
�����������ò���Ӧ����35��ԭ���ϣ����ܻ������������������10370Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ʻ������һ���£�30�죩ij���ʻ���������������������ͳ�����£����������������������Ƶ����Ϊ���ʣ�
����������֦�� |
|
|
|
|
|
�������� | 3�� | 5�� | 13�� | 6�� | 3�� |
��1��������30����������������100֦�ĸ��ʣ�
��2�����˻�����������������100֦��ʱ��ѡ��2���������������2��ǡ������������������50֦ʱ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() .
.
��1��������![]() ���溯������ʵ��
���溯������ʵ��![]() ��ֵ��
��ֵ��
��2�����������ʵ��![]() ������
������![]() ��
��![]() Ϊʵ��������ͼ���뺯��
Ϊʵ��������ͼ���뺯��![]() ��ͼ����������һ������.
��ͼ����������һ������.
�� ��![]() ��
��![]() ��ֵ��
��ֵ��
�� ��![]() �ϵ�����ʵ��
�ϵ�����ʵ��![]() ������
������![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
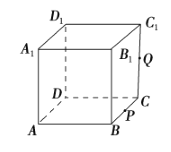
����Ŀ����ͼ��������![]() ���ⳤΪ 1��
���ⳤΪ 1�� ![]() Ϊ
Ϊ![]() ���е㣬
���е㣬 ![]() Ϊ�߶�
Ϊ�߶�![]() �ϵĶ��㣬����A��P��Q��ƽ��ظ����������õĽ����Ϊ
�ϵĶ��㣬����A��P��Q��ƽ��ظ����������õĽ����Ϊ![]() .������������ȷ����__________(д��������ȷ����ı��)��
.������������ȷ����__________(д��������ȷ����ı��)��
�ٵ�![]() ʱ��
ʱ�� ![]() Ϊ�ı��Σ��ڵ�
Ϊ�ı��Σ��ڵ�![]() ʱ��
ʱ�� ![]() Ϊ�������Σ��۵�
Ϊ�������Σ��۵�![]() ʱ��
ʱ�� ![]() Ϊ�����Σ��ܵ�
Ϊ�����Σ��ܵ�![]() ʱ��
ʱ�� ![]() �����Ϊ
�����Ϊ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��֪![]() ����ֱ������ϵ
����ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ����������������ԭ��
Ϊ����������������ԭ��![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ����ļ�����ϵ�У�ֱ��
���������Ϊ����ļ�����ϵ�У�ֱ��![]() �ļ����귽����
�ļ����귽����![]() .
.
������֤�� ![]() ��
��
�������![]() �ļ�����Ϊ
�ļ�����Ϊ![]() ��
�� ![]() Ϊֱ��
Ϊֱ��![]() ��
�� ![]() �Ľ��㣬��
�Ľ��㣬��![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪһ������壬�����ABCDΪ�����Σ�PD��ƽ��ABCD��EC��PD����PD=AD=2EC=2��
��1���뻭���ü����������ͼ��
��2��������B��CEPD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�ƽ��PAD��ƽ��ABCD��AB=AD����BAD=60�㣬E��F�ֱ���AP��AD���е㣬��֤��
��1��ֱ��EF��ƽ��PCD��
��2��ƽ��BEF��ƽ��PAD��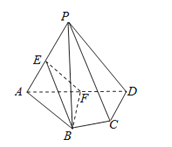
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ����
����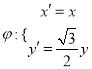 �任�������
�任�������![]() .
.
��1����![]() �ķ��̣�
�ķ��̣�
��2����![]() ����
Ϊ����![]() �����㣬
�����㣬 ![]() Ϊ����ԭ�㣬ֱ��
Ϊ����ԭ�㣬ֱ��![]() ��б�ʷֱ�Ϊ
��б�ʷֱ�Ϊ![]() ��
��![]() ����ֱ��
����ֱ��![]() ��Բ
��Բ![]() �ص��ҳ������ֵ����ʱֱ��
�ص��ҳ������ֵ����ʱֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() ����������
����������![]() ��һ�����棬�˽�������
��һ�����棬�˽�������![]() ���ڵ�
���ڵ�![]() ��
�� ![]() ,����
,����![]() �ֱ�Ϊ��
�ֱ�Ϊ��![]() ��һ��.
��һ��.
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣬��������
��һ�㣬��������![]() ������
������![]() �������ȣ���
�������ȣ���![]() �ij�.
�ij�.

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com