
【题目】已知命题α:函数![]() 的定义域是R;命题β:在R上定义运算:xy=x(1-y).不等式(x-a)(x+a)<1对任意实数x都成立.
的定义域是R;命题β:在R上定义运算:xy=x(1-y).不等式(x-a)(x+a)<1对任意实数x都成立.
(1)若α、β中有且只有一个真命题,求实数a的取值范围;
(2)若α、β中至少有一个真命题,求实数a的取值范围;
(3)若α、β中至多有一个真命题,求实数a的取值范围.
【答案】(1) (![]()
![]() ,0)∪[
,0)∪[![]() ,4);(2) (
,4);(2) (![]()
![]() ,4);(3) (
,4);(3) (![]() ∞,0)∪[
∞,0)∪[![]() ,+∞)
,+∞)
【解析】
分别求出命题α为真时和命题β为真时a的取值范围,再求:(1)若α为真、β为假时和α为假、β为真时对应a的取值范围,求并集即可;(2)求出α为假且β为假时a的取值范围,再求补集即可;(3)求出α为真且β为真时a的取值范围,再求补集即可.
函数![]() 的定义域是R,则ax2
的定义域是R,则ax2![]() ax+1>0恒成立,
ax+1>0恒成立,
a=0时,满足条件;
a≠0时,则![]() ,解得0<a<4;
,解得0<a<4;
所以命题α为真命题时,a∈[0,4);
又在R上定义运算:xy=x(1![]() y),
y),
不等式(x![]() a)(x+a)<1可化为(x
a)(x+a)<1可化为(x![]() a)(1
a)(1![]() x
x![]() a)<1,
a)<1,
即x2![]() x
x![]() a2+a+1>0对任意的x∈R都成立;
a2+a+1>0对任意的x∈R都成立;
令△=1![]() 4(
4(![]() a2+a+1)<0,
a2+a+1)<0,
解得![]()
![]() <a<
<a<![]() ,
,
所以命题β为真时a的取值范围是a∈(![]()
![]() ,
,![]() ).
).
(1)若α为真、β为假时,有 ,即
,即![]() ≤a<4;
≤a<4;
若α为假、β为真时,有 ,即
,即![]()
![]() <a<0;
<a<0;
综上,实数a的取值范围是(![]()
![]() ,0)∪[
,0)∪[![]() ,4);
,4);
(2)若α为假且β为假时,有 ,即a≤
,即a≤![]()
![]() 或a≥4;
或a≥4;
所以α、β中至少有一个真命题时,实数a的取值范围是(![]()
![]() ,4);
,4);
(3)若α为真且β为真时,有 ,即0≤a<
,即0≤a<![]() ;
;
所以α、β中至多有一个真命题时,实数a的取值范围是(![]() ∞,0)∪[
∞,0)∪[![]() ,+∞).
,+∞).


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,点
,点![]() ,直线
,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
,![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与曲线
与曲线![]() 恰有两个不同的交点,记
恰有两个不同的交点,记![]() 的所有可能取值构成集合
的所有可能取值构成集合![]() ,
,![]() 是椭圆
是椭圆![]() 上一动点,点
上一动点,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,记
对称,记![]() 的所有可能取值构成集合
的所有可能取值构成集合![]() ,若随机从集合
,若随机从集合![]() 中分别抽出一个元素
中分别抽出一个元素![]() ,则
,则![]() 的概率是___.
的概率是___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 同时满足:(1)对于定义域上的任意
同时满足:(1)对于定义域上的任意![]() ,恒有
,恒有![]() ;(2)对于定义域上的任意
;(2)对于定义域上的任意![]() ,
,![]() ,当
,当![]() 时,恒有,
时,恒有,![]() 则称函数
则称函数![]() 为“理想函数”.给出下列四个函数中:①
为“理想函数”.给出下列四个函数中:①![]() ; ②
; ②![]() ; ③
; ③![]() ;④
;④ ,则被称为“理想数”的有________(填相应的序号).
,则被称为“理想数”的有________(填相应的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知几何体![]() ,其中四边形
,其中四边形![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为矩形,
为矩形, ![]() ,且
,且![]() ,
, ![]() .
.
(1)试判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,请说明理由;
,请说明理由;
(2)若![]() ,求该几何体的表面积.
,求该几何体的表面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
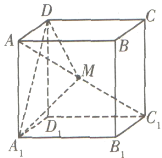
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(点
上的动点(点![]() 与
与![]() 不重合),则下列结论正确的是____.
不重合),则下列结论正确的是____.
①存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
③![]() 的面积不可能等于
的面积不可能等于![]() ;
;
④若![]() 分别是
分别是![]() 在平面
在平面![]() 与平面
与平面![]() 的正投影的面积,则存在点
的正投影的面积,则存在点![]() ,使得
,使得![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com