练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (2014·嘉兴模拟)已知a=,b=0.3-2,c=lo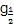2,则a,b,c的大小关系是(　　)

    A．a>b>cB．a>c>bC．c>b>aD．b>a>c

    D

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    （5分）（2011•广东）设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（（f•g）（x）对任意x∈R，（f°g）（x）=f（g（x））；（f•g）（x）=f（x）g（x），则下列等式恒成立的是（       ）

    A．（（f°g）•h）（x）=（（f•h）°（g•h））（x）
    B．（（f•g）°h）（x）=（（f°h）•（g°h））（x）
    C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
    D．（（f•g）•h）（x）=（（f•h）•（g•h））（x）

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    幂指函数y＝f(x)g(x)在求导数时，可以运用对数法：在函数解析式两边求对数得，两边求导数得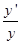＝，于是y′＝f(x)g(x)·．运用此法可以探求得知y＝的一个单调递增区间为(　　)．

    A．(0,2)B．(2,3)C．(e,4)D．(3, 8)

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知函数，若，且，则的最小值为（　）.

    A． B． C．2  D．4 

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    定义：若存在常数，使得对定义域内的任意两个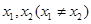，均有 成立，则称函数在定义域上满足利普希茨条件.若函数满足利普希茨条件，则常数的最小值为（ ）

    A．4 B．3 C．1 D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若直角坐标平面内的两个不同的点满足条件：①都在函数的图象上；②关于原点对称.则称点对为函数的一对“友好点对”.（注：点对与为同一“友好点对”）.已知函数，此函数的友好点对有（  ）

    A．0对　B．1对C．2对D．3对

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    函数y＝2|x|的定义域为[a，b]，值域为[1,16]，当a变化时，函数b＝g(a)的图象可以是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知f(x)＝ax－2，g(x)＝loga|x|(a>0，且a≠1)，且f(2 011)·g(－2 011)<0，则y＝f(x)，y＝g(x)在同一坐标系内的大致图象是           (　　)
      

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    定义max{s1，s2，…，sn}表示实数s1，s2，…，sn中的最大者．设A＝(a1，a2，a3)，B＝，记A?B＝max{a1b1，a2b2，a3b3}．设A＝(x－1，x＋1,1)，B＝，若A?B＝x－1，则x的取值范围为(　　)

    A．[1－，1]
    B．[1,1＋]
    C．[1－，1]
    D．[1,1＋]

    查看答案和解析>>

    同步练习册答案