
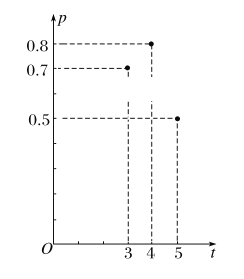
【题目】加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系![]() (a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为________分钟.
(a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为________分钟.
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,AB=4 ![]() ,AD=2
,AD=2 ![]() ,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.
,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.
(1)当θ=90°时,求A′C的长;
(2)当cosθ= ![]() 时,求BC与平面A′BD所成角的正弦值.
时,求BC与平面A′BD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
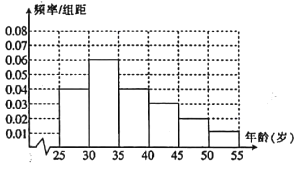
【题目】某高校进行社会实践,对![]() 岁的人群随机抽取1000人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到各年龄段人数的频率分布直方图如图所示,其中在
岁的人群随机抽取1000人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到各年龄段人数的频率分布直方图如图所示,其中在![]() 岁、
岁、![]() 岁年龄段人数中,“时尚族”人数分别占本组人数的80%、60%.
岁年龄段人数中,“时尚族”人数分别占本组人数的80%、60%.
请完成以下问题:
(1)求![]() 岁与
岁与![]() 岁年龄段“时尚族”的人数;
岁年龄段“时尚族”的人数;
(2)从![]() 岁和
岁和![]() 岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队,求领队的两人年龄都在
岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队,求领队的两人年龄都在![]() 岁内的概率.
岁内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为实数集R,及整数k、T;
(1)若函数f(x)=2xsin(πx),证明f(x+2)=4f(x);
(2)若f(x+T)=kf(x),且f(x)=axφ(x)(其中a为正的常数),试证明:函数φ(x)为周期函数;
(3)若f(x+6)= ![]() f(x),且当x∈[﹣3,3]时,f(x)=
f(x),且当x∈[﹣3,3]时,f(x)= ![]() (x2﹣9),记Sn=f(2)+f(6)+f(10)+…+f(4n﹣2),n∈N+ , 求使得S1、S2、S3、…、Sn小于1000都成立的最大整数n.
(x2﹣9),记Sn=f(2)+f(6)+f(10)+…+f(4n﹣2),n∈N+ , 求使得S1、S2、S3、…、Sn小于1000都成立的最大整数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3200元时,可全部租出。当每辆车的月租金每增加50元时(租金增减为50元的整数倍),未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)设租金为(3200+50x)元/辆(x∈N),用x表示租赁公司的月收益y(单位:元)。
(3)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx+a.
(1)若函数y=f(x)在x=e处的切线方程为y=2x,求实数a的值;
(2)设m>0,当x∈[m,2m]时,求f(x)的最小值;
(3)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),其中
为参数),其中![]() .
. ![]() 与
与![]() 交于点
交于点![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com