【题目】已知函数
， 
．
（1）求函数
的单调递增区间；
（2）若
， 
，且
， 
， 
，求实数
的取值范围．
【答案】(1) 函数
的单调递增区间为
;(2) 
.
【解析】试题分析：（1）
, 解得
,从而得到增区间；（2）
， 
， 
等价于
对
恒成立，或
对
恒成立，而
，只需研究
的符号情况即可.
试题解析：
（1）依题意， 
，
令
，解得
，故函数
的单调递增区间为
．
（2）当
，对任意的
，都有
；
当
时，对任意的
，都有
；
故
对
恒成立，或
对
恒成立，
而
，设函数
， 
．
则
对
恒成立，或
对
恒成立， 
，
①当
时，∵
,∴
，∴
恒成立，
∴
在
上单调递增， 
，
故
在
上恒成立，符合题意．
②当
时，令
，得
，令
，得
，
故
在
上单调递减，所以
，
而
，设函数
， 
，
则
，令
，则
（
）恒成立，
∴
在
上单调递增，∴
恒成立，
∴
在
上单调递增，∴
恒成立，
即
，而
，不合题意．
综上，故实数
的取值范围为
.
初中学业考试导与练系列答案科目：高中数学 来源： 题型：
【题目】若（2x+ 
）100=a0+a1x+a2x2+…+a100x100 ， 则（a0+a2+a4+…+a100）2﹣（a1+a3+a5+…+a99）2的值为（ ）
A.1
B.﹣1
C.0
D.2
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f（x）=1﹣
,求解：（1）f（x）的值域；（2）证明f（x）为R上的增函数． ．
（1）求f（x）的值域；
（2）证明f（x）为R上的增函数．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f（x）=ex﹣ax（a∈R），e为自然对数的底数．
（1）若a=1时，求曲线y=f（x）在x=0处的切线方程；
（2）求函数f（x）在[0，1]上的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数．他们研究过如图所示的三角形数：
将三角形数1，3，6，10，…记为数列{an}，将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn}，可以推测：
（1）b5=；
（2）b2n﹣1= ．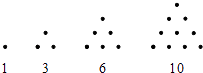 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义方程f（x）=f′（x）的实数根x0叫做函数f（x）的“异驻点”．若函数g（x）=2016x，h（x）=ln（x+1），φ（x）=x3﹣1的“异驻点”分别为α，β，γ，则α，β，γ的大小关系为（ ）
A.α＞β＞γ
B.β＞α＞γ
C.β＞γ＞α
D.γ＞α＞β
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ） 
在某一个周期内的图象时，列表并填入了部分数据，如表：
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
f（x）=Asin（ωx+φ） | 0 | 5 | ﹣5 | 0 |
（1）请将如表数据补充完整，并直接写出函数f（x）的解析式；
（2）将函数y=f（x）的图象向左平移 
个单位长度，得到函数y=g（x）的图象，求y=g（x）的图象离原点O最近的对称中心．
（3）求当 
时，函数y=g（x）的值域．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
