
【题目】已知圆C1:x2+y2﹣3x﹣3y+3=0,圆C2:x2+y2﹣2x﹣2y=0,求两圆的公共弦所在的直线方程及弦长.
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】一个盒子里装有标号为1,2,3,…,5的5张标签,现随机地从盒子里无放回地抽取两张标签.记X为两张标签上的数字之和.
(1)求X的分布列.
(2)求X的期望E(X)和方差D(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
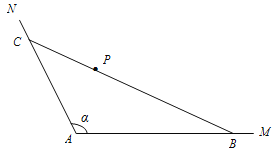
【题目】如图(示意),公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
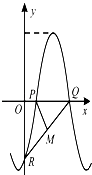
【题目】如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤ ![]() )的图象与坐标轴的三个交点为P,Q,R,且P(1,0),Q(m,0)(m>0),∠PQR=
)的图象与坐标轴的三个交点为P,Q,R,且P(1,0),Q(m,0)(m>0),∠PQR= ![]() ,M为QR的中点,|PM|=
,M为QR的中点,|PM|= ![]() .
. 
(1)求m的值及f(x)的解析式;
(2)设∠PRQ=θ,求tanθ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体ABCD﹣A1B1C1D1中,E、F分别是AA1、AB的中点,则EF与对角面A1C1CA所成角的度数是( )
A.30°
B.45°
C.60°
D.150°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1和双曲线C2焦点相同,且离心率互为倒数,F1 , F2它们的公共焦点,P是椭圆和双曲线在第一象限的交点,当∠F1PF2=60°时,则椭圆C1的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 在直角坐标系
在直角坐标系![]() 中的参数方程为
中的参数方程为![]() 为参数,
为参数, ![]() 为倾斜角),以坐标原点
为倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,在极坐标系中,曲线的方程为
轴正半轴为极轴,建立极坐标系,在极坐标系中,曲线的方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求使
两点,求使![]() 为定值的
为定值的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com