
【题目】设椭圆C: ![]() 的一个顶点与抛物线
的一个顶点与抛物线![]() 的焦点重合,
的焦点重合, ![]() 分别是椭圆的左、右焦点,且离心率
分别是椭圆的左、右焦点,且离心率![]() ,过椭圆右焦点
,过椭圆右焦点![]() 的直线l与椭圆C交于
的直线l与椭圆C交于![]() 两点.
两点.
(1)求椭圆C的方程;
(2)若![]() ,求直线l的方程;
,求直线l的方程;
(3)若![]() 是椭圆C经过原点O的弦,
是椭圆C经过原点O的弦, ![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1) ![]() ;(2) y=
;(2) y=![]() (x-1)或y=-
(x-1)或y=-![]() (x-1);(3)见解析.
(x-1);(3)见解析.
【解析】试题分析:(1)由题意,椭圆的标准方程为![]() +
+![]() =1;(2)设直线l的方程为y=k(x-1)(k≠0),
=1;(2)设直线l的方程为y=k(x-1)(k≠0),![]() ·
·![]() =x1x2+y1y2=-2,利用韦达定理,解得答案;(3)|MN|=
=x1x2+y1y2=-2,利用韦达定理,解得答案;(3)|MN|=![]() |x1-x2|,|AB|=
|x1-x2|,|AB|=![]() |x3-x4|,代入韦达定理计算,得到答案。
|x3-x4|,代入韦达定理计算,得到答案。
试题解析:
(1)椭圆的顶点为(0,![]() ),即b=
),即b=![]() ,e=
,e=![]() =
=![]() ,∴a=2,∴椭圆的标准方程为
,∴a=2,∴椭圆的标准方程为![]() +
+![]() =1.
=1.
(2)由题可知,直线l与椭圆必相交.
①当直线斜率不存在时,经检验不合题意.
②当斜率存在时,设直线l的方程为y=k(x-1)(k≠0),
且M(x1,y1),N(x2,y2).
由 得(3+4k2)x2-8k2x+4k2-12=0,x1+x2=
得(3+4k2)x2-8k2x+4k2-12=0,x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
![]() ·
·![]() =x1x2+y1y2=x1x2+k2[x1x2-(x1+x2)+1]
=x1x2+y1y2=x1x2+k2[x1x2-(x1+x2)+1]
=![]() +k2
+k2![]()
=![]() =-2,解得k=±
=-2,解得k=±![]() ,
,
故直线l的方程为y=![]() (x-1)或y=-
(x-1)或y=-![]() (x-1).
(x-1).
(3)证明:设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4),
由(2)可得|MN|=![]() |x1-x2|
|x1-x2|
=![]()
=![]()
=![]() ,
,
由 消去y并整理得x2=
消去y并整理得x2=![]() ,
,
|AB|=![]() |x3-x4|=4
|x3-x4|=4![]() ,
,
∴![]() =
= =4,为定值.
=4,为定值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知:三棱锥![]() 中,侧面
中,侧面![]() 垂直底面,
垂直底面, ![]() 是底面最长的边;图1是三棱锥
是底面最长的边;图1是三棱锥![]() 的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥
的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥![]() 的直观图的一部分,其中点
的直观图的一部分,其中点![]() 在
在![]() 平面内.
平面内.
(Ⅰ)请在图2中将三棱锥![]() 的直观图补充完整,并指出三棱锥
的直观图补充完整,并指出三棱锥![]() 的哪些面是直角三角形;
的哪些面是直角三角形;![]()
![]()
(Ⅱ)设二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值;
的值;
(Ⅲ)求点![]() 到面
到面![]() 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图像如图所示,则下列结论中一定成立的是( )
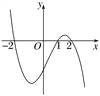
A. 函数f(x)有极大值f(2)和极小值f(1) B. 函数f(x)有极大值f(-2)和极小值f(1)
C. 函数f(x)有极大值f(2)和极小值f(-2) D. 函数f(x)有极大值f(-2)和极小值f(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,三个点
,三个点![]() ,
, ![]() ,
, ![]() 中恰有两个点在
中恰有两个点在![]() 上.
上.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过![]() 的直线交
的直线交![]() 于
于![]() ,
, ![]() 两点,点
两点,点![]() 为
为![]() 上任意一点,证明:直线
上任意一点,证明:直线![]() ,
, ![]() ,
, ![]() 的斜率成等差数列.
的斜率成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某大型景区有两条直线型观光路线![]() ,
, ![]() ,
,![]() ,点
,点![]() 位于
位于![]() 的平分线上,且与顶点
的平分线上,且与顶点![]() 相距1公里.现准备过点
相距1公里.现准备过点![]() 安装一直线型隔离网
安装一直线型隔离网![]() (
(![]() 分别在
分别在![]() 和
和![]() 上),围出三角形区域
上),围出三角形区域![]() ,且
,且![]() 和
和![]() 都不超过5公里.设
都不超过5公里.设![]() ,
, ![]() (单位:公里).
(单位:公里).
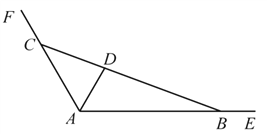
(Ⅰ)求![]() 的关系式;
的关系式;
(Ⅱ)景区需要对两个三角形区域![]() ,
, ![]() 进行绿化.经测算,
进行绿化.经测算, ![]() 区城每平方公里的绿化费用是
区城每平方公里的绿化费用是![]() 区域的两倍,试确定
区域的两倍,试确定![]() 的值,使得所需的总费用最少.
的值,使得所需的总费用最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:min)的频率分布直方图,若将日均课外阅读时间不低于60 min的学生称为“书虫”,低于60 min的学生称为“懒虫”,

(1)求x的值并估计全校3 000名学生中“书虫”大概有多少名学生?(将频率视为概率)
(2)根据已知条件完成下面2×2的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“书虫”与性别有关:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究患肺癌与是否吸烟有关,某肿瘤机构随机抽取了40人做相关调查,其中不吸烟人数与吸烟人数相同,已知吸烟人数中,患肺癌与不患肺癌的比为![]() ;不吸烟的人数中,患肺癌与不患肺癌的比为
;不吸烟的人数中,患肺癌与不患肺癌的比为![]() .
.
(1)现从患肺癌的人中用分层抽样的方法抽取5人,再从这5人中随机抽取2人进行调查,求这两人都是吸烟患肺癌的概率;
(2)是否有99.9%的把握认为患肺癌与吸烟有关?
附: 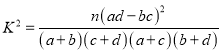 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的双曲线![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,(
,( ![]() 为原点)
为原点)
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() :
: ![]() 与双曲线恒有两个不同的交点
与双曲线恒有两个不同的交点![]() 和
和![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 关于
关于![]() 轴对称,顶点在坐标原点
轴对称,顶点在坐标原点![]() ,直线
,直线![]() 经过抛物线
经过抛物线![]() 的焦点.
的焦点.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若不经过坐标原点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,且满足
,且满足![]() ,证明直线
,证明直线![]() 过
过![]() 轴上一定点
轴上一定点![]() ,并求出点
,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com