练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知A、B、C分别是△ABC的三个内角，且cosA•cos（A-B）=cosB．
    （1）求证：△ABC是等腰三角形；
    （2）若tanA=2，求tanC的值．

    解：（1）由已知，得cosA（cosAcosB+sinAsinB）=cosB，
    即（1-cos2A）cosB=sinAcosAsinB，
    亦即sin2AcosB=sinAcosAsinB．
    因为sinA＞0，所以sinAcosB=cosAsinB，
    于是sin（A-B）=0．
    又-π＜A-B＜π，从而A=B．
    故△ABC是等腰三角形．
    （2）在△ABC中，有C=π-（A+B）=π-2A，
    所以tanC=tan（π-2A）=-tan2A．
    由tanA=2得tan2A==-
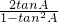
    所以tanC的值为．
    分析：（1）先利用两角差的余弦公式将已知三角恒等式展开，进而利用同角三角函数基本关系式及倒用两角差的正弦公式，结合三角形中角的取值范围即可得三角形角间的关系，进而判断三角形形状；（2）由（1）可知A=B，故利用诱导公式和三角形内角和定理可得tanC=-tan2A，进而利用二倍角的正切公式求得结果
    点评：本题考查了三角变换公式在化简函数式中的应用，三角形形状的判断方法，解三角形的知识
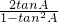    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知a、b、c分别是△ABC三个内角A、B、C的对边．
    （1）若b2=ac，求角B的范围．
    （2）若acosA=bcosB，试判断△ABC的形状，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若a=1，b=
    		3
    ，A+C=2B，则sinC=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a、b、c分别是△ABC的三个内角A、B、C所对的边，若
    cosB
    cosC
    =-
    b
    2a+c
    ，则B=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a，b，c分别是△ABC中角A，B，C的对边，且sin2A+sin2C-sin2B=sinAsinC．
     （1）求角B的大小；
     （2）若c=3a，求tanA的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a，b，c分别是△ABC的三个内角A，B，C的对边，且满足2asinB-
    		3
    b=0．
    （Ⅰ）求角A的大小；
    （Ⅱ）当A为锐角时，求函数y=
    		3
    sinB+sin（C-
    π
    6
    ）的最大值．

    查看答案和解析>>

    同步练习册答案