
科目:高中数学 来源: 题型:填空题
 -
- =1(a>0,b>0)的右焦点为F,过F做双曲线C的一条渐近线的垂线,与双曲线交于M,垂足为N,若M为线段FN的中点,则双曲线C的离心率为 ________.
=1(a>0,b>0)的右焦点为F,过F做双曲线C的一条渐近线的垂线,与双曲线交于M,垂足为N,若M为线段FN的中点,则双曲线C的离心率为 ________.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 为了解地震灾区高三学生的身体发育状况,抽查了该地区100名年龄为17岁~18岁的男生体重(kg),得到如图频率分布直方图.根据图中所示知体重在[56.5,64.5)的学生人数有
为了解地震灾区高三学生的身体发育状况,抽查了该地区100名年龄为17岁~18岁的男生体重(kg),得到如图频率分布直方图.根据图中所示知体重在[56.5,64.5)的学生人数有查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
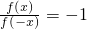 .
.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
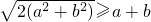 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com