
【题目】如图,正方体![]() 的棱长为2,P为BC的中点,Q为线段
的棱长为2,P为BC的中点,Q为线段![]() 上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是______(写出所有正确命题的编号).
上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是______(写出所有正确命题的编号).

①当![]() 时,S为四边形;②当
时,S为四边形;②当![]() 时,S为等腰梯形;③当
时,S为等腰梯形;③当![]() 时,S与
时,S与![]() 的交点R满足
的交点R满足![]() ;④当
;④当![]() 时,S为五边形;⑤当
时,S为五边形;⑤当![]() 时,S的面积为
时,S的面积为![]() .
.
【答案】①②④
【解析】
利用空间几何元素的位置关系和截面的性质逐一分析推理判断每一个命题的真假得解.
对于①,由图1知,
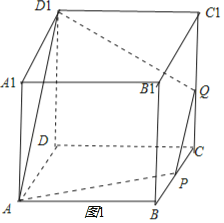
当点Q向C移动时,满足0<CQ<1,只需在DD1上取点M,且满足AM∥PQ,
则截面图形为四边形APQM,∴①正确;
对于②,当CQ=1时,即Q为CC1中点,此时可得PQ∥AD1,AP=QD1=![]() ,
,
可得截面APQD1为等腰梯形,∴②正确;
对于③,当CQ=![]() 时,如图2所示,
时,如图2所示,
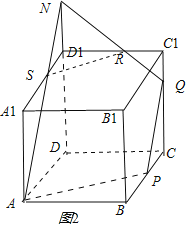
延长DD1至N,使D1N=1,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,
可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1Q:D1N=1:2,可得C1R=![]() ,D1R=
,D1R=![]() ,∴③错误;
,∴③错误;
对于④,当![]() 时,只需点Q上移,此时的截面形状仍然上图所示的APQRS,是五边形,④正确;
时,只需点Q上移,此时的截面形状仍然上图所示的APQRS,是五边形,④正确;
对于⑤,当CQ=2时,Q与C1重合,取A1D1的中点F,连接AF,可证PC1∥AF,且PC1=AF,
可知截面为APC1F为菱形,且面积为![]() AC1PF=2
AC1PF=2![]() ,⑤错误;
,⑤错误;
综上可得:正确命题的序号为①②④.
故答案为:①②④.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,如图所示点
,如图所示点![]() 为椭圆上任意三点.
为椭圆上任意三点.

(Ⅰ)若![]() ,是否存在实数
,是否存在实数![]() ,使得代数式
,使得代数式![]() 为定值.若存在,求出实数
为定值.若存在,求出实数![]() 和
和![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅱ)若![]() ,求三角形
,求三角形![]() 面积的最大值;
面积的最大值;
(Ⅲ)满足(Ⅱ),且在三角形![]() 面积取得最大值的前提下,若线段
面积取得最大值的前提下,若线段![]() 与椭圆长轴和短轴交于点
与椭圆长轴和短轴交于点![]() (
(![]() 不是椭圆的顶点).判断四边形
不是椭圆的顶点).判断四边形![]() 的面积是否为定值.若是,求出定值;若不是,说明理由.
的面积是否为定值.若是,求出定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】剪纸艺术是最古老的中国民间艺术之一,作为一种镂空艺术,它能给人以视觉上以透空的感觉和艺术享受.在中国南北方的剪纸艺术,通过一把剪刀、一张纸、就可以表达生活中的各种喜怒哀乐.如图是一边长为1的正方形剪纸图案,中间黑色大圆与正方形的内切圆共圆心,圆与圆之间是相切的,且中间黑色大圆的半径是黑色小圆半径的2倍,若在正方形图案上随机取一点,则该点取自白色区域的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,点(an,an+1)在直线y=x+2上,且首项a1=1.
(1)求数列{an}的通项公式;
(2)数列{an}的前n项和为Sn,等比数列{bn}中,b1=a1,b2=a2,数列{bn}的前n项和为Tn,请写出适合条件Tn≤Sn的所有n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在各棱长均为2的三棱柱![]() 中,侧面
中,侧面![]() 底面ABC,
底面ABC,![]() .
.
(1)求侧棱![]() 与平面
与平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)已知点D满足![]() ,在直线
,在直线![]() 上是否存在点P,使DP∥平面
上是否存在点P,使DP∥平面![]() ?若存在,请确定点P的位置,若不存在,请说明理由.
?若存在,请确定点P的位置,若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某自行车手从O点出发,沿折线O﹣A﹣B﹣O匀速骑行,其中点A位于点O南偏东45°且与点O相距20 ![]() 千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°﹣α)(其中sinα=
千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°﹣α)(其中sinα= ![]() ,0°<α<90°)且与点O相距5
,0°<α<90°)且与点O相距5 ![]() 千米(假设所有路面及观测点都在同一水平面上).
千米(假设所有路面及观测点都在同一水平面上).
(1)求该自行车手的骑行速度;
(2)若点O正西方向27.5千米处有个气象观测站E,假定以点E为中心的3.5千米范围内有长时间的持续强降雨.试问:该自行车手会不会进入降雨区,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个三棱锥的三视图是三个直角三角形,如图所示,则该三棱锥的外接球的表面积为__________.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395438592/STEM/3d69fcdc50254164a6fb81896ba4fb1c.png]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com