
分析 (Ⅰ)设P点的坐标为(x,y),求出直线的斜率,利用斜率乘积,化简求解即可.
(Ⅱ)当直线l的斜率不存在时,直线的方程为x=1,求出两个三角形的面积,判断相等,当直线l的斜率存在时,
法1:设直线的方程为y=k(x-1),P(x1,y1),Q(x2,y2).联立直线与椭圆方程,求出M,N坐标,通过△BPQ和△BMN的面积不相等,推出结果.
法2:设直线的方程为y=k(x-1),P(x1,y1),Q(x2,y2).联立直线与椭圆方程,通过S△BPQ=S△BMN,得到$\frac{|BP|}{|BM|}=\frac{|BN|}{|BQ|}$.推出-1=0.说明△BPQ和△BMN的面积不相等.
解答 (本题满分9分)
解:(Ⅰ)设P点的坐标为(x,y),
则${k_{PA}}=\frac{y}{x+2}(x≠-2)$,${k_{PB}}=\frac{y}{x-2}(x≠2)$.
∵${k_{PA}}•{k_{PB}}=-\frac{1}{4}$,∴$\frac{y^2}{{{x^2}-4}}=-\frac{1}{4}(x≠±2)$.
化简得曲线C的轨迹方程为$\frac{x^2}{4}+{y^2}=1(x≠±2)$. …(4分)
(Ⅱ)当直线l的斜率不存在时,直线的方程为x=1,则$P(1,\frac{{\sqrt{3}}}{2}),Q(1,-\frac{{\sqrt{3}}}{2})$.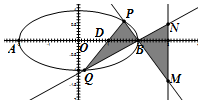
直线PB的方程为$y=-\frac{{\sqrt{3}}}{2}(x-2)$,解得$M(3,-\frac{{\sqrt{3}}}{2})$.
直线QB的方程为$y=\frac{{\sqrt{3}}}{2}(x-2)$,解得$N(3,\frac{{\sqrt{3}}}{2})$.
则${S_{△BPQ}}=\frac{1}{2}×\sqrt{3}×1=\frac{{\sqrt{3}}}{2}$,${S_{△BMN}}=\frac{1}{2}×\sqrt{3}×1=\frac{{\sqrt{3}}}{2}$.
此时△BPQ和△BMN的面积相等 …(6分)
当直线l的斜率存在时,
法1:设直线的方程为y=k(x-1),P(x1,y1),Q(x2,y2).
由$\left\{{\begin{array}{l}{y=k(x-1)}\\{{x^2}+4{y^2}=4}\end{array}}\right.$得(1+4k2)x2-8k2x+4k2-4=0.${x_1}+{x_2}=\frac{{8{k^2}}}{{1+4{k^2}}}$,${x_1}{x_2}=\frac{{4{k^2}-4}}{{1+4{k^2}}}$.
直线PB的方程为$y=\frac{y_1}{{{x_1}-2}}(x-2)$,求得$M(3,\frac{y_1}{{{x_1}-2}})$.
直线QB的方程为$y=\frac{y_2}{{{x_2}-2}}(x-2)$,求得$N(3,\frac{y_2}{{{x_2}-2}})$.${S_{△BPQ}}=\frac{1}{2}|PQ|h=\frac{1}{2}\sqrt{1+{k^2}}|{x_1}-{x_2}|×\frac{|k|}{{\sqrt{1+{k^2}}}}=\frac{1}{2}|k||{x_1}-{x_2}|$,${S_{△BMN}}=\frac{1}{2}|MN|h=\frac{1}{2}|{y_N}-{y_M}|=\frac{1}{2}|\frac{{k({x_1}-{x_2})}}{{({x_1}-2)({x_2}-2)}}|$.
若S△BPQ=S△BMN,则(2-x1)(2-x2)=1,即x1x2-2(x1+x2)+3=0.
∴$\frac{{4{k^2}-4}}{{1+4{k^2}}}-\frac{{16{k^2}}}{{1+4{k^2}}}+3=0$,化简得-1=0.
此式不成立.所以△BPQ和△BMN的面积不相等
综上,直线l的方程为x=1. …(9分)
法2:设直线的方程为y=k(x-1),P(x1,y1),Q(x2,y2).
由$\left\{{\begin{array}{l}{y=k(x-1)}\\{{x^2}+4{y^2}=4}\end{array}}\right.$得(1+4k2)x2-8k2x+4k2-4=0.${x_1}+{x_2}=\frac{{8{k^2}}}{{1+4{k^2}}}$,${x_1}{x_2}=\frac{{4{k^2}-4}}{{1+4{k^2}}}$.${S_{△BPQ}}=\frac{1}{2}|BQ||BP|sin∠PBQ$,${S_{△BMN}}=\frac{1}{2}|BM||BN|sin∠MBN$,
因为∠PBQ=∠MBN,S△BPQ=S△BMN,
所以|BQ||BP|=|BM||BN|,即$\frac{|BP|}{|BM|}=\frac{|BN|}{|BQ|}$.
则有$\frac{{2-{x_1}}}{3-2}=\frac{3-2}{{2-{x_2}}}$,化简得x1x2-2(x1+x2)+3=0.
∴$\frac{{4{k^2}-4}}{{1+4{k^2}}}-\frac{{16{k^2}}}{{1+4{k^2}}}+3=0$,化简得-1=0.
此式不成立.所以△BPQ和△BMN的面积不相等
综上,直线l的方程为x=1. …(9分)
点评 本题考查直线与椭圆的位置关系的综合应用,轨迹方程的求法,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,e) | B. | (0,e) | C. | (e,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}R$ | B. | $\frac{{\sqrt{3}}}{2}R$ | C. | $\sqrt{2}R$ | D. | $\frac{{\sqrt{2}}}{2}R$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com