
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 上各点的纵坐标伸长为原来的
上各点的纵坐标伸长为原来的![]() 倍(横坐标不变)得到曲线
倍(横坐标不变)得到曲线![]() ,求
,求![]() 的参数方程;
的参数方程;
(2)若![]() ,
,![]() 分别是直线
分别是直线![]() 与曲线
与曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 过点
过点![]() ,
,![]() 为其焦点,过
为其焦点,过![]() 且不垂直于
且不垂直于![]() 轴的直线
轴的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,动点
两点,动点![]() 满足
满足![]() 的垂心为原点
的垂心为原点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)求证:动点![]() 在定直线
在定直线![]() 上,并求
上,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知四边形
中,已知四边形![]() 是边长为
是边长为![]() 的正方形,点
的正方形,点![]() 在底面
在底面![]() 上的射影为底面
上的射影为底面![]() 的中心点
的中心点![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() 的面积为1.
的面积为1.
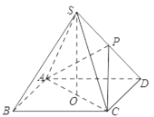
(1)若点![]() 是
是![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() 使得二面角
使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业参加![]() 项目生产的工人为
项目生产的工人为![]() 人,平均每人每年创造利润
人,平均每人每年创造利润![]() 万元.根据现实的需要,从
万元.根据现实的需要,从![]() 项目中调出
项目中调出![]() 人参与
人参与![]() 项目的售后服务工作,每人每年可以创造利润
项目的售后服务工作,每人每年可以创造利润![]() 万元(
万元(![]() ),
),![]() 项目余下的工人每人每年创造利图需要提高
项目余下的工人每人每年创造利图需要提高![]()
(1)若要保证![]() 项目余下的工人创造的年总利润不低于原来
项目余下的工人创造的年总利润不低于原来![]() 名工人创造的年总利润,则最多调出多少人参加
名工人创造的年总利润,则最多调出多少人参加![]() 项目从事售后服务工作?
项目从事售后服务工作?
(2)在(1)的条件下,当从![]() 项目调出的人数不能超过总人数的
项目调出的人数不能超过总人数的![]() 时,才能使得
时,才能使得![]() 项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数
项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{2n﹣1}的前n项1,3,7,…,2n﹣1组成集合![]() (n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
(n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 满足
满足![]() .
.
①存在![]() 可以生成的数列
可以生成的数列![]() 是常数数列;
是常数数列;
②“数列![]() 中存在某一项
中存在某一项![]() ”是“数列
”是“数列![]() 为有穷数列”的充要条件;
为有穷数列”的充要条件;
③若![]() 为单调递增数列,则
为单调递增数列,则![]() 的取值范围是
的取值范围是![]() ;
;
④只要![]() ,其中
,其中![]() ,则
,则![]() 一定存在;
一定存在;
其中正确命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》全称《新编直指算法统宗》,是屮国古代数学名著,程大位著.书中有如下问题:“今有五人均银四十两,甲得十两四钱,戊得五两六钱.问:次第均之,乙丙丁各该若干?”意思是:有5人分40两银子,甲分10两4钱,戊分5两6钱,且相邻两项差相等,则乙丙丁各分几两几钱?(注:1两等于10钱)( )
A.乙分8两,丙分8两,丁分8两B.乙分8两2钱,丙分8两,丁分7两8钱
C.乙分9两2钱,丙分8两,丁分6两8钱D.乙分9两,丙分8两,丁分7两
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个无穷数列![]() 分别满足
分别满足![]() ,
,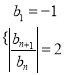 ,
,
其中![]() ,设数列
,设数列![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,
(1)若数列![]() 都为递增数列,求数列
都为递增数列,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:存在唯一的正整数
满足:存在唯一的正整数![]() (
(![]() ),使得
),使得![]() ,称数列
,称数列![]() 为“
为“![]() 坠点数列”
坠点数列”
①若数列![]() 为“5坠点数列”,求
为“5坠点数列”,求![]() ;
;
②若数列![]() 为“
为“![]() 坠点数列”,数列
坠点数列”,数列![]() 为“
为“![]() 坠点数列”,是否存在正整数
坠点数列”,是否存在正整数![]() ,使得
,使得![]() ,若存在,求
,若存在,求![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com