
在三棱锥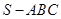 中,
中, ,
,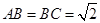 ,
,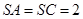 ,二面角
,二面角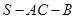 的余弦值是
的余弦值是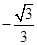 ,若
,若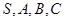 都在同一球面上,则该球的表面积是.
都在同一球面上,则该球的表面积是.
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:填空题
如图是从上下底面处在水平状态下的棱长为 的正方体
的正方体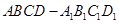 中分离出来的.
中分离出来的.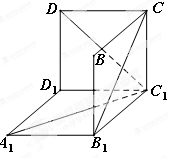
有如下结论:
① 在图中的度数和它表示的角的真实度数都是
在图中的度数和它表示的角的真实度数都是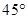 ;
;
②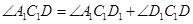 ;
;
③ 与
与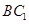 所成的角是
所成的角是 ;
;
④若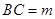 ,则用图示中这样一个装置盛水,最多能盛
,则用图示中这样一个装置盛水,最多能盛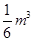 的水.
的水.
其中正确的结论是 (请填上你所有认为正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
如图,正方体ABCD A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号).
A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号). 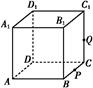
①当0<CQ< 时,S为四边形;
时,S为四边形;
②当CQ= 时,S为等腰梯形;
时,S为等腰梯形;
③当CQ= 时,S与C1D1的交点R满足C1R=
时,S与C1D1的交点R满足C1R=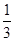 ;
;
④当 <CQ<1时,S为六边形;
<CQ<1时,S为六边形;
⑤当CQ=1时,S的面积为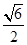 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知某一多面体内接于一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com