
| ѡ�� | ѧ������ |
| A | 20 |
| B | 30 |
| C | 40 |
| D | 60 |
���� ��1�����ó�����ֱ�����A��B��C��D���ſγ�ȡѧ������
��2����������˼ά���ӳ�ȡ��15��ѧ�����������ȡ2�ˣ���2�˵�ѡ��ǡ�ò�ͬ�ĸ��ʣ�
��3���ж�X=0��1��2��3��������ʣ�Ȼ�����ֲ����Լ��������ɣ�
��� ����С������12�֣�
�⣺��1���ֲ�����ķ�������ѡȡ15�ˣ���������150�������ȣ�$\frac{1}{10}$��
Ӧ�ֱ��A��B��C��D���ſ��и���ȡ��ѧ������Ϊ2��3��4��6�ˣ�����2�֣�
��2����2�˵�ѡ��ǡ�ò�ͬ�ĸ���Ϊ��$P=1-\frac{C_2^2}{{C_{15}^2}}-\frac{C_3^2}{{C_{15}^2}}-\frac{C_4^2}{{C_{15}^2}}-\frac{C_6^2}{{C_{15}^2}}$����4�֣�
=$\frac{16}{21}$������6�֣�
��3����������֪��X=0��1��2��3������8�֣�$P��X=0��=\frac{C_6^3}{{C_{10}^3}}=\frac{20}{120}$��$P��X=1��=\frac{C_4^1C_6^2}{{C_{10}^3}}=\frac{60}{120}$��$P��X=2��=\frac{C_4^2C_6^1}{{C_{10}^3}}=\frac{36}{120}$��$P��X=3��=\frac{C_4^3}{{C_{10}^3}}=\frac{4}{120}$������10�֣�
X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 |
| P | $\frac{20}{120}$ | $\frac{60}{120}$ | $\frac{36}{120}$ | $\frac{4}{120}$ |
���� ���⿼��ֲ������Ӧ�ã���ɢ����������ķֲ����Լ����������������������


 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $2\sqrt{3}$ | B�� | $3\sqrt{2}$ | C�� | $\sqrt{15}$ | D�� | $\sqrt{13}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
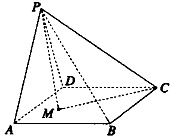 ��ͼ��������P-ABCD�У�����PADΪ�������Σ�����ABCD�DZ߳�Ϊ2�������Σ�����PAD�͵���ABCD��MΪ����ABCD�ڵ�һ�����㣬������MP=MC�����M��������ABCD�ڵĹ켣�ij���Ϊ$\sqrt{5}$��
��ͼ��������P-ABCD�У�����PADΪ�������Σ�����ABCD�DZ߳�Ϊ2�������Σ�����PAD�͵���ABCD��MΪ����ABCD�ڵ�һ�����㣬������MP=MC�����M��������ABCD�ڵĹ켣�ij���Ϊ$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ʾһ���㷨����ʼ�ͽ������������ | |
| B�� | ��ʾһ���㷨������������Ϣ��������� | |
| C�� | ��ʾһ���㷨����ʼ�ͽ������������ | |
| D�� | ��ʾһ���㷨������������Ϣ��������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��k��5 | B�� | k��4 | C�� | k��1 | D�� | k��2��k��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com