
【题目】把单位正方体的六个面分别染上6种颜色,并画上个数不同的金鸡,各面的颜色与鸡的个数对应如表:
面上所染颜色 | 红 | 黄 | 蓝 | 青 | 紫 | 绿 |
该面上的金鸡个数 | 1 | 2 | 3 | 4 | 5 | 6 |
取同样的4个上述的单位正方体拼成一个如图所示的水平放置的长方体.则这个长方体的下底面总计画有______个金鸡

科目:高中数学 来源: 题型:
【题目】某创业团队拟生产![]() 两种产品,根据市场预测,
两种产品,根据市场预测,![]() 产品的利润与投资额成正比(如图1),
产品的利润与投资额成正比(如图1),![]() 产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)
产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)

(注:利润与投资额的单位均为万元)
(1)分別将![]() 两种产品的利润
两种产品的利润![]() 、
、![]() 表示为投资额
表示为投资额![]() 的函数;
的函数;
(2)该团队已筹集到10 万元资金,并打算全部投入![]() 两种产品的生产,问:当
两种产品的生产,问:当![]() 产品的投资额为多少万元时,生产
产品的投资额为多少万元时,生产![]() 两种产品能获得最大利润,最大利润为多少?
两种产品能获得最大利润,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C, AB=3,BC=5.
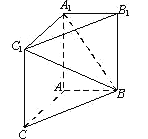
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;
(3)求点C到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017全国Ⅱ,文19)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:

旧养殖法
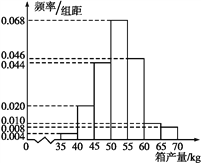
新养殖法
(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关;
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,AD∥BC,∠BAD=![]() ,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2.
,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2.
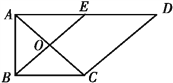
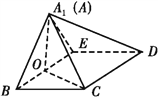
图1 图2
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某海滨浴场海浪的高度y(米)是时间t(0≤t≤24,单位:时)的函数,记作:![]() .下表是某日各时的浪高数据.
.下表是某日各时的浪高数据.
t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1)根据以上数据,求函数y=f(t)的函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com