
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)设函数![]() (其中
(其中![]() 为
为![]() 的导函数),判断
的导函数),判断![]() 在
在![]() 上的单调性;
上的单调性;
(2)若函数![]() 在定义域内无零点,试确定正数
在定义域内无零点,试确定正数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 在
在![]() 上单调递增.(2)
上单调递增.(2)![]() .
.
【解析】
(1)先分析得到![]() ,即得函数
,即得函数![]() 在
在![]() 上的单调性;(2)先利用导数求出
上的单调性;(2)先利用导数求出
![]() ,再对a分三种情况讨论,讨论每一种情况下的零点情况得解.
,再对a分三种情况讨论,讨论每一种情况下的零点情况得解.
(1)因为![]() ,则
,则![]() ,
,
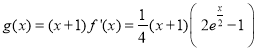 ,
,
∴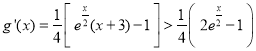
 ,
,
∴![]() 在
在![]() 上单调递增.
上单调递增.
(2)由![]() 知
知![]() ,
,
由(1)知![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,可知当
,可知当![]() 时,
时,![]() ,
,
则![]() 有唯一零点,设此零点为
有唯一零点,设此零点为![]() ,
,
易知![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
故![]() ,其中
,其中![]() .
.
令![]() ,
,
则![]()
![]() ,
,
易知![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() ,
,![]() 在
在![]() 上单调递增,且
上单调递增,且![]() .
.
①当![]() 时,
时,![]() ,由
,由![]() 在
在![]() 上单调递增知
上单调递增知![]() ,
,
则![]() ,由
,由![]() 在
在![]() 上单调递增,
上单调递增,![]() ,所以
,所以![]() ,故
,故![]() 在
在![]() 上有零点,不符合题意;
上有零点,不符合题意;
②当![]() 时,
时,![]() ,由
,由![]() 的单调性知
的单调性知![]() ,则
,则![]() ,此时
,此时![]() 有一个零点,不符合题意;
有一个零点,不符合题意;
③当![]() 时,
时,![]() ,由
,由![]() 的单调性知
的单调性知![]() ,则
,则![]() ,此时
,此时![]() 没有零点.
没有零点.
综上所述,当![]() 无零点时,正数
无零点时,正数![]() 的取值范围是
的取值范围是![]() .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】某公司近年来科研费用支出![]() 万元与公司所获得利润
万元与公司所获得利润![]() 万元之间有如下的统计数据:
万元之间有如下的统计数据:
x | 2 | 3 | 4 | 5 |
Y | 18 | 27 | 32 | 35 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)试根据(1)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式:
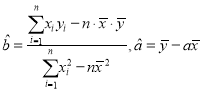
参考数据:2×18+3×27+4×32+5×35=420
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,长轴长为4,离心率为
,长轴长为4,离心率为![]() .过右焦点
.过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(均不与
两点(均不与![]() 重合),记直线
重合),记直线![]()
![]() 的斜率分别为
的斜率分别为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在常数![]() ,当直线
,当直线![]() 变动时,总有
变动时,总有![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种,
方案一:每满200元减50元;
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、l个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 半价 | 7折 | 8折 | 原价 |
(1)若两个顾客都选择方案二,各抽奖一次,求至少一个人获得半价优惠的概率;
(2)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() )以坐标原点为极点,
)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 和
和![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com