
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(2)对一切![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)探讨函数![]() 是否存在零点?若存在,求出函数
是否存在零点?若存在,求出函数![]() 的零点;若不存在,请说明理由.
的零点;若不存在,请说明理由.
【答案】(1) 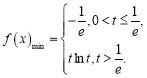 ;(2)
;(2) ![]() ;(3) 函数
;(3) 函数![]() 无零点.
无零点.
【解析】
试题分析:(1)求函数![]() 的层数可得
的层数可得![]() ,并由导数的符号判断函数的单调性可得函数在区间
,并由导数的符号判断函数的单调性可得函数在区间![]() 上的最小值为
上的最小值为![]() ,分别讨论当
,分别讨论当![]() 与
与![]() 时函数在区间
时函数在区间![]() 上的单调性与最小值即可;(2)对一切
上的单调性与最小值即可;(2)对一切![]() ,
,![]() 恒成立
恒成立![]() ,构造函数
,构造函数![]() ,求函数
,求函数![]() 的最小值即可;(3)
的最小值即可;(3) ![]()
![]()
![]() ,由(Ⅰ)知当且仅当
,由(Ⅰ)知当且仅当![]() 时,
时,![]() 的最小值是
的最小值是![]() ,构造函数
,构造函数![]() ,求其导数,研究函数
,求其导数,研究函数![]() 的单调性与最值可知
的单调性与最值可知![]() ,且两个函数取得最大值点与最小值点时不相等,所以有
,且两个函数取得最大值点与最小值点时不相等,所以有![]() ,即两个函数无公共点,即函数
,即两个函数无公共点,即函数![]() 无零点.
无零点.
试题解析: (Ⅰ)![]() ,
,
由![]() 得,
得,![]() ,由
,由![]() 得
得![]() ,
,
![]() 函数
函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.………………(1分)
上单调递增.………………(1分)
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,………………(2分)
,………………(2分)
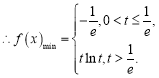 ………………(3分)
………………(3分)
(Ⅱ)原问题可化为![]() ,………………(4分)
,………………(4分)
设![]() ,
,
![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上单调递减;…………(5分)
上单调递减;…………(5分)
当![]() 时,
时,![]() 在
在![]() 上单调递增;………………(6分)
上单调递增;………………(6分)
![]() ,故
,故![]() 的取值范围为
的取值范围为![]() .………………(7分)
.………………(7分)
(Ⅲ)令![]() ,得
,得![]() ,即
,即![]() ,………………(8分)
,………………(8分)
当(Ⅰ)知当且仅当![]() 时,
时,![]() 的最小值是
的最小值是![]() ,…………(9分)
,…………(9分)
设![]() ,则
,则![]() ,易知
,易知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
![]() 当且仅当
当且仅当![]() 时,
时,![]() 取最大值,且
取最大值,且![]() ,………………(10分)
,………………(10分)
![]() 对
对![]() 都有
都有![]() ,即
,即![]() 恒成立,
恒成立,
故函数![]() 无零点.……………………(12分)
无零点.……………………(12分)


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.

(1)若![]() =6
=6![]() ,求k的值;
,求k的值;
(2)求四边形AEBF面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为![]() ,宽为
,宽为![]() 的长方形铁皮做一个无盖的容器.先在四角分别截去一个小正方形,然后把四边翻转
的长方形铁皮做一个无盖的容器.先在四角分别截去一个小正方形,然后把四边翻转![]() ,再焊接而成(如图).问该容器的高为多少时,容器的容积最大?最大容积是多少?
,再焊接而成(如图).问该容器的高为多少时,容器的容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=elnx,g(x)=![]() f(x)-(x+1).(e=2.718……)
f(x)-(x+1).(e=2.718……)
(1)求函数g(x)的极大值;
(2)求证:1+![]() +
+![]() +…+
+…+![]() >ln(n+1)(n∈N*).
>ln(n+1)(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,两焦点
,两焦点![]() ,点
,点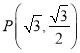 在椭圆
在椭圆![]() 上.
上.

(1)求椭圆![]() 的方程;
的方程;
(2)如图,动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,点
有且仅有一个公共点,点![]() 、
、![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() .求四边形
.求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ),将
),将![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到
个单位长度后得到![]() 的图象,且
的图象,且![]() 在区间
在区间![]() 内的最大值为
内的最大值为![]() .
.
(1)求实数![]() 的值;
的值;
(2)在![]() 中,内角
中,内角![]() ,
, ![]() ,
, ![]() 的对边分别是
的对边分别是![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,且
,且![]() ,求
,求![]() 的周长
的周长![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
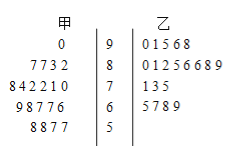
(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀,请填写下面的![]() 列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
下面临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| span>2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com