
【题目】若四面体ABCD的三组对棱分别相等,即![]() ,
,![]() ,
,![]() ,给出下列结论:
,给出下列结论:
①四面体ABCD每组对棱相互垂直;
②四面体ABCD每个面的面积相等;
③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于![]() 而小于
而小于![]() ;
;
④连接四面体ABCD每组对棱中点的线段相互垂直平分;
⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长.
其中正确结论的序号是( )
A.②④⑤B.①②④⑤C.①③④D.②③④⑤
【答案】A
【解析】
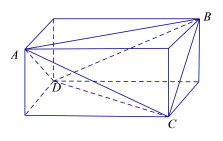
把该四面体补成一个长方体,然后根据长方体对每个命题进行判断.
由于四面体ABCD的三组对棱分别相等,因此可以把它补成一个长方体,如图.
由长方体知:
长方体的每个面是矩形,对角线不一定垂直,因此四面体![]() 的对棱不一定垂直,①错;
的对棱不一定垂直,①错;
四面体的四个面是全等三角形,因此面积相等,②正确;
由于四面体的四个面是全等三角形,因此每个顶点出发的三条棱两两夹角之和这180°,③错;
由四面体每条棱中点是所在长方体的面上的对角线交点,长方体对面对角线交点的连线互相垂直平分,即四面体每组对棱中点的连线段相互垂直平分,④正确;
四面体的每个面三角形的三边长就等于从同一点出发的三条棱的长度,⑤正确.
因此有②④⑤正确.
故选:A.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)将曲线![]() 上所有点的横坐标不变,纵坐标缩短到原来的
上所有点的横坐标不变,纵坐标缩短到原来的![]() 倍,得到曲线
倍,得到曲线![]() ,若
,若![]() 与
与![]() 的交点为
的交点为![]() (异于坐标原点
(异于坐标原点![]() ),
),![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年起,福建省高考将实行“3+1+2”新高考.“3”是统一高考的语文、数学和英语三门;“1”是选择性考试科目,由考生在物理、历史两门中选一门;“2”也是选择性考试科目,由考生从化学、生物、地理、政治四门中选择两门,则某考生自主选择的“1+2”三门选择性考试科目中,历史和政治均被选择到的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形ABCD,E,F分别为AB,CD的中点,将△ADE沿DE折起,使△ACD为等边三角形,如图所示,记二面角A-DE-C的大小为![]() .
.
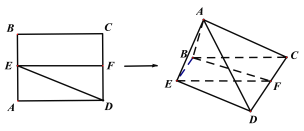
(1)证明:点A在平面BCDE内的射影G在直线EF上;
(2)求角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是AC的中点,四边形BDEF是菱形,平面![]() 平面ABC,
平面ABC,![]() ,
,![]() ,
,![]() .
.

![]() 若点M是线段BF的中点,证明:
若点M是线段BF的中点,证明:![]() 平面AMC;
平面AMC;
![]() 求平面AEF与平面BCF所成的锐二面角的余弦值.
求平面AEF与平面BCF所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,点
,点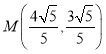 在椭圆C上,延长
在椭圆C上,延长![]() 交椭圆于N点.
交椭圆于N点.
(1)求椭圆C的方程;
(2)P,Q为椭圆上的点,记线段MN,PQ的中点分别为A,B(A,B异于原点O),且直线AB过原点O,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式(4kx﹣k2﹣12k﹣9)(2x﹣11)>0,其中k∈R,对于不等式的解集A,记B=A∩Z(其中Z为整数集),若集合B是有限集,则使得集合B中元素个数最少时的实数k的取值范围是__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com