
【题目】已知函数f(x)=|2x-1|+|x+m|.
(l)当m=l时,解不等式f(x)≥3;
(2)证明:对任意x∈R,2f(x)≥|m+1|-|m|.
【答案】(1){x|x≤-1或x≥1};(2)见解析
【解析】
(1)根据绝对值定义将不等式化为三个不等式组,分别求解,最后求并集,(2)根据绝对值三角不等式放缩论证.
(1)当m=1时,f(x)=|2x-1|+|x+1|,
①当x≤-1时,f(x)=-3x≥3,解得x≤-1,
②当-1<x<![]() 时,f(x)=-x+2≥3,解得x≤-1,与-1<x<
时,f(x)=-x+2≥3,解得x≤-1,与-1<x<![]() 矛盾,舍去,
矛盾,舍去,
③当x≥![]() 时,f(x)=3x≥3,解得x≥1,
时,f(x)=3x≥3,解得x≥1,
综上,不等式f(x)<3的解集为{x|x≤-1或x≥1};
(2)2f(x)=|4x-2|+|2x+2m|=|2x-1|+|2x-1|+|2x+2m|≥|2x-1|+|2x+2m|≥|2x+2m-2x+1|
=|2m+1|=|(m+1)+m|≥|m+1|-|m|,
∴对任意x∈R,2f(x)≥|m+1|-|m|.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
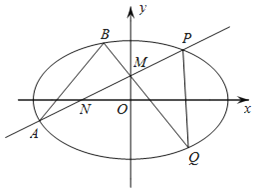
【题目】如图,已知椭圆![]() ,过动点M(0,m)的直线交x轴于点N,交椭圆C于A,P(其中P在第一象限,N在椭圆内),且M是线段PN的中点,点P关于x轴的对称点为Q,延长QM交C于点B,记直线PM,QM的斜率分别为k1,k2.
,过动点M(0,m)的直线交x轴于点N,交椭圆C于A,P(其中P在第一象限,N在椭圆内),且M是线段PN的中点,点P关于x轴的对称点为Q,延长QM交C于点B,记直线PM,QM的斜率分别为k1,k2.
(1)当![]() 时,求k2的值;
时,求k2的值;
(2)当![]() 时,求直线AB斜率的最小值.
时,求直线AB斜率的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对边分别为a、b、c,且2acosC=2b-c.
(1)求角A的大小;
(2)若AB=3,AC边上的中线SD的长为![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
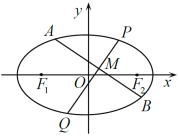
【题目】如图,![]() 、
、![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]() :
:![]() 的左、右焦点,过
的左、右焦点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 所得弦长为
所得弦长为![]() ,设
,设![]() 、
、![]() 是椭圆
是椭圆![]() 上的两个动点,线段
上的两个动点,线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 的横坐标为1.
的横坐标为1.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
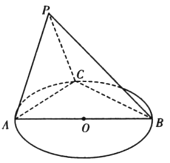
【题目】如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,平面PAC垂直圆O所在平面,直线PC与圆O所在平面所成角为60°,PA⊥PC.
(1)证明:AP⊥平面PBC
(2)求二面角P—AB一C的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
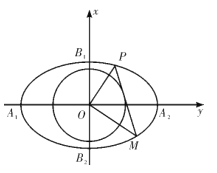
【题目】如图,已知椭圆![]() 的左、右顶点为
的左、右顶点为![]() ,
,![]() ,上、下顶点为
,上、下顶点为![]() ,
,![]() ,记四边形
,记四边形![]() 的内切圆为
的内切圆为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() 的一条不与坐标轴平行的切线
的一条不与坐标轴平行的切线![]() 交椭圆
交椭圆![]() 于P,M两点.
于P,M两点.
(i)求证:![]() ;
;
(ii)试探究![]() 是否为定值.
是否为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com