
【题目】已知A,B是抛物线C:y2=4x上两点,线段AB的垂直平分线与x轴有唯一的交点P(x0,0).
(1)求证:x0>2;
(2)若直线AB过抛物线C的焦点F,且|AB|=10,求|PF|.
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】已知点Pn(an,bn)满足an+1=an·bn+1,bn+1=![]() (n∈N*),且点P1的坐标为(1,-1).
(n∈N*),且点P1的坐标为(1,-1).
(1)求过点P1,P2的直线l的方程;
(2)试用数学归纳法证明:对于n∈N*,点Pn都在(1)中的直线l上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() (
(![]() 是常数,且
是常数,且![]() ).
).
(1)讨论函数![]() 的单调区间;
的单调区间;
(2)当![]() 在
在![]() 处取得极值时,若关于
处取得极值时,若关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数![]() 的取值范围;
的取值范围;
(3)求证:当![]() ,
,![]() 时,
时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100名学生的数学成绩,发现都在![]() 内现将这100名学生的成绩按照
内现将这100名学生的成绩按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组后,得到的频率分布直方图如图所示,则下列说法正确的是
分组后,得到的频率分布直方图如图所示,则下列说法正确的是![]()
![]()

A. 频率分布直方图中a的值为![]()
B. 样本数据低于130分的频率为![]()
C. 总体的中位数![]() 保留1位小数
保留1位小数![]() 估计为
估计为![]() 分
分
D. 总体分布在![]() 的频数一定与总体分布在
的频数一定与总体分布在![]() 的频数相等
的频数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一块各面均涂有油漆的正方体被锯成27个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,从中任意取出一个,则取出的小正方体两面涂有油漆的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较两位运动员甲和乙的打靶成绩,在相同条件下测得各打靶![]() 次所得环数(已按从小到大排列)如下:
次所得环数(已按从小到大排列)如下:
甲的环数:![]()
乙的环数:![]()
(1)完成茎叶图,并分别计算两组数据的平均数及方差;

(2)(i)根据(1)的结果,分析两人的成绩;
(ii)如果你是教练,请你作出决策:根据对手实力的强弱分析应该派两人中的哪一位上场比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,以极轴为
,以极点为原点,以极轴为![]() 轴的正半轴,取相同的单位长度,建立平面直角坐标系,直线
轴的正半轴,取相同的单位长度,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为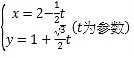 .
.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 上任一点为
上任一点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是根据某行业网站统计的某一年1月到12月(共12个月)的山地自行车销售量(![]() 代表1000辆)折线图,其中横轴代表月份,纵轴代表销售量,由折线图提供的数据回答下列问题:
代表1000辆)折线图,其中横轴代表月份,纵轴代表销售量,由折线图提供的数据回答下列问题:
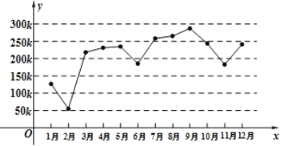
(1)在一年中随机取一个月的销售量,估计销售量不足![]() 的概率;
的概率;
(2)在一年中随机取连续两个月的销售量,估计这连续两个月销售量递增(如2月到3月递增)的概率;
(3)根据折线图,估计年平均销售量在哪两条相邻水平平行线线之间(只写出结果,不要过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com