
分析 先设P(x,y)是曲线y=$\sqrt{x}$上的任一点,P1(x′,y′)是P(x,y)在矩阵M对应变换作用下新曲线上的对应点,根据矩阵变换求出P与P1的关系,代入已知曲线求出所求曲线即可.
解答 解:设P(x,y)是曲线y=$\sqrt{x}$的任一点,
P1(x′,y′)是P(x,y)在矩阵y=$\sqrt{x}$对应变换作用下新曲线上的对应点,则$\left\{\begin{array}{l}{x=y′}\\{y=x′}\end{array}\right.$
代入曲线y=$\sqrt{x}$,得x′=$\sqrt{y′}$,
即y′=x′2
曲线y=$\sqrt{x}$在矩阵$[\begin{array}{l}{0}&{1}\\{1}&{0}\end{array}]$作用下变换的结果是曲线方程y=x2,
故答案为:y=x2.
点评 本题主要考查了几种特殊的矩阵变换,以及轨迹方程等有关知识,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
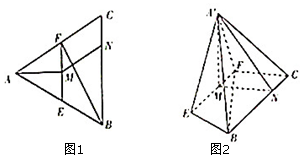 如图,已知等边△ABC中,E,F分别为AB,AC边的中点,M为EF的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.
如图,已知等边△ABC中,E,F分别为AB,AC边的中点,M为EF的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com