
 的左焦点,A,B分别是椭圆的两个顶点,椭圆的离心率为
的左焦点,A,B分别是椭圆的两个顶点,椭圆的离心率为 ,点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线
,点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线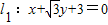 相切
相切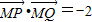 ,求直线l2的方程.
,求直线l2的方程.
 ,所以
,所以 ,所以
,所以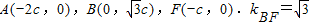 ,故
,故 ,所以BC得方程为
,所以BC得方程为 ,由此入手能得到所求的椭圆方程.
,由此入手能得到所求的椭圆方程.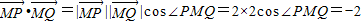 ,所以∠PMQ=120°.所以M到直线l2的距离等于1.依题意,直线l2的斜率存在,设直线l2:y=k(x+2),所以
,所以∠PMQ=120°.所以M到直线l2的距离等于1.依题意,直线l2的斜率存在,设直线l2:y=k(x+2),所以 ,由此能得到所求的直线l2的方程.
,由此能得到所求的直线l2的方程. ,所以
,所以 ,即
,即 (2分)
(2分) ,故
,故 ,
, (4分)
(4分)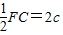 ,圆心M(c,0)
,圆心M(c,0) 相切,
相切, =2c,∴c=1,∴a=2,b=
=2c,∴c=1,∴a=2,b=
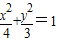 (8分)
(8分)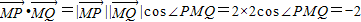 ,
, ,解得
,解得 ,
, (15分)
(15分)

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:2009-2010学年浙江省杭州十四中高三(上)11月月考数学试卷(理科)(解析版) 题型:解答题
 的左焦点,A,B分别是椭圆的两个顶点,椭圆的离心率为
的左焦点,A,B分别是椭圆的两个顶点,椭圆的离心率为 ,点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线
,点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线 相切
相切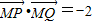 ,求直线l2的方程.
,求直线l2的方程.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省常州中学高三最后冲刺综合练习数学试卷2(文科)(解析版) 题型:解答题
 的左焦点,A,B分别是椭圆的两个顶点,椭圆的离心率为
的左焦点,A,B分别是椭圆的两个顶点,椭圆的离心率为 ,点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线
,点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线 相切
相切 ,求直线l2的方程.
,求直线l2的方程.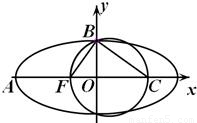
查看答案和解析>>
科目:高中数学 来源:2010年江苏省盐城市东台中学高考数学模拟试卷(二)(解析版) 题型:解答题
 的左焦点,A,B分别是椭圆的两个顶点,椭圆的离心率为
的左焦点,A,B分别是椭圆的两个顶点,椭圆的离心率为 ,点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线
,点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线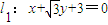 相切
相切 ,求直线l2的方程.
,求直线l2的方程.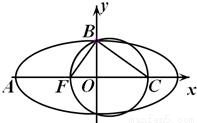
查看答案和解析>>
科目:高中数学 来源:2010年高考数学模拟试卷(2)(解析版) 题型:解答题
 的左焦点,A,B分别是椭圆的两个顶点,椭圆的离心率为
的左焦点,A,B分别是椭圆的两个顶点,椭圆的离心率为 ,点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线
,点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线 相切
相切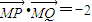 ,求直线l2的方程.
,求直线l2的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com