
【题目】设![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求![]() 的值;
的值;
(2)若对于任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)a=0(2)m≥1
【解析】试题分析:(1)先求导数,再根据导数几何意义得f′(1)=1,求得![]() 的值;(2)先分离变量
的值;(2)先分离变量![]() ,再利用导数研究函数
,再利用导数研究函数![]() 单调性,最后根据洛必达法则求函数最大值,即得
单调性,最后根据洛必达法则求函数最大值,即得![]() 的取值范围.
的取值范围.
试题解析:(1)f′(x)=
由题设f′(1)=1,∴![]() ,∴a=0.
,∴a=0.
(2)![]() ,x∈[1,+∞),f(x)≤m(x﹣1),
,x∈[1,+∞),f(x)≤m(x﹣1),
即4lnx≤m(3x﹣![]() ﹣2)
﹣2)
设g(x)=4lnx﹣m(3x﹣![]() ﹣2),即x∈[1,|+∞),g(x)≤0,
﹣2),即x∈[1,|+∞),g(x)≤0,
∴g′(x)=![]() ﹣m(3+
﹣m(3+![]() )=
)=![]() ,g′(1)=4﹣4m
,g′(1)=4﹣4m
①若m≤0,g′(x)>0,g(x)≥g(1)=0,这与题设g(x)≤0矛盾
②若m∈(0,1),当x∈(1,![]() ),g′(x)>0,g(x)单调递增,g(x)≥g(1)=0,与题设矛盾.
),g′(x)>0,g(x)单调递增,g(x)≥g(1)=0,与题设矛盾.
③若m≥1,当x∈(1,+∞),),g′(x)≤0,g(x)单调递减,g(x)≤g(1)=0,即不等式成立
综上所述,m≥1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点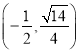 ,且离心率为
,且离心率为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 的右顶点,探究:
的右顶点,探究: ![]() 是否为定值,若是,求出该定值,若不是,请说明理由.(其中,
是否为定值,若是,求出该定值,若不是,请说明理由.(其中, ![]() ,
, ![]() 分别是直线
分别是直线![]() 、
、![]() 的斜率)
的斜率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中, PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1, ![]() ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.
(Ⅰ)求证:AD⊥CG;
(Ⅱ)求平面BCP与平面DCP的夹角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,记随机变量
个,记随机变量![]() 表示质量在
表示质量在![]() 内的芒果个数,求
内的芒果个数,求![]() 的分布列及数学期望.
的分布列及数学期望.
(2)以各组数据的中间数代表这组数据的平均值,将频率视为概率,某经销商来收购芒果,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若满足条件:存在
,若满足条件:存在![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ,则称
,则称![]() 为“倍缩函数”.若函数
为“倍缩函数”.若函数![]() 为“倍缩函数”,则实数
为“倍缩函数”,则实数![]() 的取值范围是
的取值范围是
A. (﹣∞,ln2﹣1) B. (﹣∞,ln2﹣1]
C. (1﹣ln2,+∞) D. [1﹣ln2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年6月深圳地铁总公司对深圳地铁1号线30个站的工作人员的服务态度进行了满意度调查,其中世界之窗、白石洲、高新园、深大、桃园、大新6个站的得分情况如下:
地铁站 | 世界之窗 | 白石州 | 高新园 | 深大 | 桃园 | 大新 |
满意度得分 | 70 | 76 | 72 | 70 | 72 | x |
已知6个站的平均得分为75分.
(1)求大新站的满意度得分x,及这6个站满意度得分的标准差;
(2)从表中前5个站中,随机地选2个站,求恰有1个站得分在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为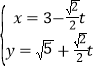 (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的圆心到直线
的圆心到直线![]() 的距离;
的距离;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构组织语文、数学学科能力竞赛,按照一定比例淘汰后,颁发一二三等奖.现有某考场的两科考试成绩数据统计如下图所示,其中数学科目成绩为二等奖的考生有![]() 人.
人.
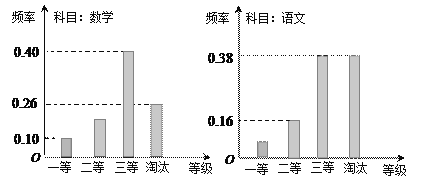

(Ⅰ)求该考场考生中语文成绩为一等奖的人数;
(Ⅱ)用随机抽样的方法从获得数学和语文二等奖的学生中各抽取![]() 人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
(Ⅲ)已知本考场的所有考生中,恰有![]() 人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取
人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取![]() 人进行访谈,求两人两科成绩均为一等奖的概率.
人进行访谈,求两人两科成绩均为一等奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com