
1 n |
2 n |
n n |
| Sn |
| 2n |
| (1+q)n |
| q |
| Sn |
| 2n |
| (1+q)n |
| q |
| Sn |
| 2n |
| Sn+1 |
| 2n+1 |
| Sn |
| 2n |
| 1 |
| q |
| 1+q |
| 2 |
| 1+q |
| 2 |
| q-1 |
| 2q |
| 1+q |
| 2 |
| bn+1 |
| bn |
| 1+q |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| A、(0,4) |
| B、(1,4] |
| C、(0,4] |
| D、[4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
 为了解某年级女生五十米短跑情况,从该年级中随机抽取8名女生进行五十跑测试,她们的测试成绩(单位:秒)的茎叶图(以整数部分为茎,小数部分为叶)如图所示.由此可估计该年级女生五十米跑成绩及格(及格成绩为9.4秒)的概率为( )
为了解某年级女生五十米短跑情况,从该年级中随机抽取8名女生进行五十跑测试,她们的测试成绩(单位:秒)的茎叶图(以整数部分为茎,小数部分为叶)如图所示.由此可估计该年级女生五十米跑成绩及格(及格成绩为9.4秒)的概率为( )| A、0.375 | B、0.625 |
| C、0.5 | D、0.125 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| 1+cos2x |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
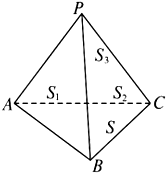 在△ABC中,射影定理可以表示为a=bcosC+ccosB,其中a,b,c依次为角A、B、C的对边.类比以上定理,如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推广到三维空间,其表现形式应为
在△ABC中,射影定理可以表示为a=bcosC+ccosB,其中a,b,c依次为角A、B、C的对边.类比以上定理,如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推广到三维空间,其表现形式应为查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(0,1) | ||
B、(0,
| ||
| C、(10,+∞) | ||
| D、(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
 从某小区抽取100个家庭进行月用电量调查,发现其月用电量都在50度至350度之间,频率分布直方图如图所示.
从某小区抽取100个家庭进行月用电量调查,发现其月用电量都在50度至350度之间,频率分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com