
 ,
, ,
, ,有下列命题:
,有下列命题: •
• )
) -(
-( •
• )
) =0
=0 |-|
|-| |<|
|<| -
- |;
|; •
• )
) -(
-( •
• )
) 不与
不与 垂直;
垂直; 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 -
- 的夹角为60°.
的夹角为60°. •
• )
) 表示一个与
表示一个与 平行的向量,而(
平行的向量,而( •
• )
) 表示一个与
表示一个与 平行的向量,故①不一定成立.
平行的向量,故①不一定成立. =
= 时,②不成立.
时,②不成立. •
• )
) -(
-( •
• )
) ]•
]• =0,得到(
=0,得到( •
• )
) -(
-( •
• )
) 与
与 垂直,故③不正确.
垂直,故③不正确. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,可得向量
|,可得向量 和
和 、
、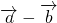 这三个向量构成一个等边三角形,故④正确.
这三个向量构成一个等边三角形,故④正确. •
• )
) 表示一个与
表示一个与 平行的向量,而(
平行的向量,而( •
• )
) 表示一个与
表示一个与 平行的向量,而
平行的向量,而 与
与 的大小方向都不确定,
的大小方向都不确定, =
= 时,|
时,| |-|
|-| |=|
|=| -
- |=0,故②不成立.
|=0,故②不成立. •
• )
) -(
-( •
• )
) ]•
]• =(
=( •
• )•(
)•( •
• )-(
)-( •
• )•(
)•( •
• )=0,故(
)=0,故( •
• )
) -(
-( •
• )
) 与
与 垂直,
垂直, 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,∴向量
|,∴向量 和
和 、
、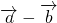 这三个向量构成一个等边三角形,
这三个向量构成一个等边三角形, 与
与 

科目:高中数学 来源:2012-2013学年安徽省马鞍山市高一(上)期末数学试卷(解析版) 题型:填空题
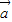 ,
, ,
, ,有下列几个命题:
,有下列几个命题: ,则
,则 或
或 ;
; 与
与 均为单位向量,它们的夹角为60°,则
均为单位向量,它们的夹角为60°,则 ;
; ,
, ,
, 满足
满足 ,
, ,则
,则 与
与 的夹角为120°;
的夹角为120°; ,
, ,则
,则 在
在 方向上的投影是-1.
方向上的投影是-1.查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省外语外贸大学附设外语学校高三(上)数学寒假作业3(文科)(解析版) 题型:选择题
 ,
, ,
, .有下列三个命题:
.有下列三个命题: •
• =
= •
• ,则
,则 =
= .
. =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省潍坊市现代中学高三(上)12月月考数学试卷(文科)(解析版) 题型:填空题
 ,
, ,
, ,有下列三个命题:
,有下列三个命题: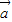 •
• =
= •
• ,则
,则 =
= 、
、 =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=|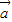 -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.查看答案和解析>>
科目:高中数学 来源:2008年陕西省高考数学试卷(文科)(解析版) 题型:解答题
 ,
, ,
, ,有下列三个命题:
,有下列三个命题: •
• =
= •
• ,则
,则 =
= 、
、 =(1,k),
=(1,k),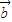 =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.查看答案和解析>>
科目:高中数学 来源:2008年陕西省高考数学试卷(理科)(解析版) 题型:解答题
 ,
, ,
, ,有下列三个命题:
,有下列三个命题: •
• =
= •
• ,则
,则 =
= 、
、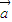 =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com