设等差数列{an}的前n项和为Sn,首项为25,且S9=S17,
求:(1)求公差d
(2)数列{an}的通项公式;
(3)求数列{an}前多少项和最大,并求其最大值.
解:设公差为d
∵等差数列{a
n}的首项为25,且s
9=s
17∴9a
1+
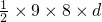
=
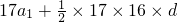
∴d=-2
(2)由(1)可知a
1=25,d=-2
∴a
n=a
1+(n-1)d=27-2n
(3)令a
n≥0,,
∴27-2n≥0
∴
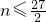
∴数列{a
n}的前13项均为正从第14项开始全为负.
∴
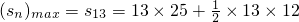
×(-2)=169
即数列{a
n}的前13项和最大且最大值为169
分析:(1)设出公差为d利用等差数列的前n项和公式代入s
9=s
17化简即可.
(2)由(1)利用等差数列的通项公式代入计算即可.
(3)可分析等差数列{a
n}哪些项是正项哪些项是0哪些项时负项因此正项或正项加0项才最大因此可令a
n≥0得出n的范围即可.
点评:本题主要考查了利用等差数列的性质求等差数列的公差,通项,数列的前n项和的最大值.前两问较简单只需知道等差数列的前n项和公式即可.而第三问要利用等差数列的性质(利用a
n≥0可得出数列{a
n}的前13项均为正从第14项开始全为负)即可求解,这一技巧在等差数列的求解中要引起注意!

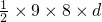 =
=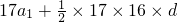
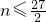
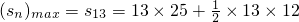 ×(-2)=169
×(-2)=169

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案