
 ,推广到空间,棱长为a的正四面体内任意一点到各个面的距离之和也为定值,则这个定值为: .
,推广到空间,棱长为a的正四面体内任意一点到各个面的距离之和也为定值,则这个定值为: . 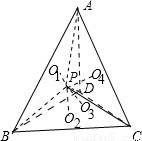 解:边长为a的等边三角形内任意一点到三边距离之和是由该三角形的面积相等得到的,
解:边长为a的等边三角形内任意一点到三边距离之和是由该三角形的面积相等得到的,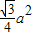 ,高为
,高为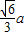 .
.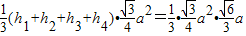 .
.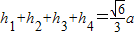 .
.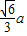 .
.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
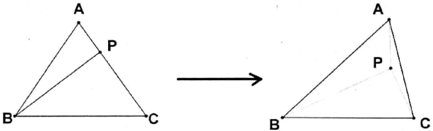
 如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是
如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是查看答案和解析>>
科目:高中数学 来源: 题型:
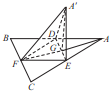 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:| 1 | 64 |
查看答案和解析>>
科目:高中数学 来源:2011学年浙江省杭州二中高考数学第一次仿真试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:专项题 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com