
【题目】如图是函数![]() 在区间
在区间![]() 上的图象,为了得到这个函数的图象,只需将y=sinx的图象
上的图象,为了得到这个函数的图象,只需将y=sinx的图象
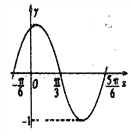
A. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
B. 向左平移至![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
C. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
D. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C1的参数方程为
中,曲线C1的参数方程为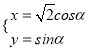 (α为参数),以原点O为极点,x轴的正半轴为级轴,建立极坐标系,曲线C2的极坐标方程
(α为参数),以原点O为极点,x轴的正半轴为级轴,建立极坐标系,曲线C2的极坐标方程![]() ;
;
(1)求曲线C1的普通方程和曲线C2的直角坐标方程;
(2)设P为曲线C1上的动点,求点P到曲线C2上的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:只要
满足:只要![]() ,必有
,必有![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列, ![]() ,
, ![]() ,
, ![]() 判断
判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(3)设![]() 是无穷数列,已知
是无穷数列,已知![]() .求证:“对任意
.求证:“对任意![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,点M的坐标为![]() ,曲线C的方程为
,曲线C的方程为![]() ;以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为
;以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为![]() 的直线l经过点M.
的直线l经过点M.
(I)求直线l和曲线C的直角坐标方程:
(II)若P为曲线C上任意一点,直线l和曲线C相交于A,B两点,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,点M的坐标为![]() ,曲线C的方程为
,曲线C的方程为![]() ;以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为
;以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为![]() 的直线l经过点M.
的直线l经过点M.
(I)求直线l和曲线C的直角坐标方程:
(II)若P为曲线C上任意一点,直线l和曲线C相交于A,B两点,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上存在一点
上存在一点![]()
![]() 到焦点
到焦点![]() 的距离等于
的距离等于![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 两点在
两点在![]() 轴上方),点
轴上方),点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,且
,且![]() ,求△
,求△![]() 的外接圆的方程.
的外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在D上的函数,若对D中的任意两数
是定义在D上的函数,若对D中的任意两数![]() ),恒有
),恒有![]() ,则称
,则称![]() 为定义在D上的C函数.
为定义在D上的C函数.
(1)试判断函数![]() 是否为定义域上的C函数,并说明理由;
是否为定义域上的C函数,并说明理由;
(2)若函数![]() 是R上的奇函数,试证明
是R上的奇函数,试证明![]() 不是R上的C函数;
不是R上的C函数;
(3)设![]() 是定义在D上的函数,若对任何实数
是定义在D上的函数,若对任何实数![]() 以及D中的任意两数
以及D中的任意两数![]() ),恒有
),恒有![]() ,则称
,则称![]() 为定义在D上的π函数. 已知
为定义在D上的π函数. 已知![]() 是R上的π函数,m是给定的正整数,设
是R上的π函数,m是给定的正整数,设![]() ,且
,且![]() ,记
,记![]() . 对于满足条件的任意函数
. 对于满足条件的任意函数![]() ,试求
,试求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com