练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

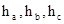    在平面上,设是三角形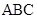三条边上的高.P为三角形内任一点,P到相应三边的距离分别为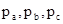,我们可以得到结论:

    试通过类比,写出在空间中的类似结论____________________________.

     

    【答案】

     

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出下列四个命题：
    ①设x1，x2∈R，则x1＞1且x2＞1的充要条件是x1+x2＞2且x1x2＞1；
    ②任意的锐角三角形ABC中，有sinA＞cosB成立；
    ③平面上n个圆最多将平面分成2n2-4n+4个部分；
    ④空间中直角在一个平面上的正投影可以是钝角．
    其中真命题的序号是
     
    （要求写出所有真命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面上，设ha，hb，hc是三角形ABC三条边上的高．P为三角形内任一点，P到相应三边的距离分别为pa，pb，pc，我们可以得到结论：
    pa
    ha
    +
    pb
    hb
    +
    pc
    hc
    =1    试通过类比，写出在空间中的类似结论
     

    查看答案和解析>>

    科目：高中数学 来源：2010年广东省高考数学冲刺预测试卷01（理科）（解析版） 题型：解答题

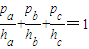    在平面上，设ha，hb，hc是三角形ABC三条边上的高．P为三角形内任一点，P到相应三边的距离分别为pa，pb，pc，我们可以得到结论：试通过类比，写出在空间中的类似结论   

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年浙江省高三上学期10月月考数学试卷 题型：填空题

    在平面上,设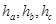是三角形ABC三条边上的高.P为三角形内任一点,P到相应三边的距离分别为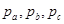,我们可以得到结论:  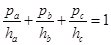类比到空间中的四面体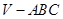内任一点p, 其中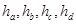为四面体四个面上的高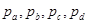，为p点到四个面的距离，我们可以得到类似结论为           

     

    查看答案和解析>>

    同步练习册答案