
 ,定点
,定点 ,M为圆上一动点,P点在TM上,N点在GM上,且满足
,M为圆上一动点,P点在TM上,N点在GM上,且满足 ,点N的轨迹为曲线E.
,点N的轨迹为曲线E. ,若△ABO的面积是
,若△ABO的面积是 ,求a值.
,求a值.
 =0可得|NM|=|NT|,∴|NG|+|NT|=|NG|+|NM|=|GM|=2a>|GT|=2
=0可得|NM|=|NT|,∴|NG|+|NT|=|NG|+|NM|=|GM|=2a>|GT|=2 a,再根据椭圆的定义可得曲线E的方程.
a,再根据椭圆的定义可得曲线E的方程. ,y1y2=
,y1y2= ,再结合
,再结合 可得y1=-2y2,即可求出y2,再利用其表示出三角形的面积,进而求出k的取值,即可得到a的取值.
可得y1=-2y2,即可求出y2,再利用其表示出三角形的面积,进而求出k的取值,即可得到a的取值. =0,
=0, a …2分
a …2分 a,0)为焦点的椭圆,且长轴长为2a,
a,0)为焦点的椭圆,且长轴长为2a, ,
, =0,
=0, …①,y1y2=
…①,y1y2= …②…6分
…②…6分 ,
, …④…8分
…④…8分  …11分
…11分 代入②③④解得:a=±
代入②③④解得:a=±


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
 已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.查看答案和解析>>
科目:高中数学 来源: 题型:
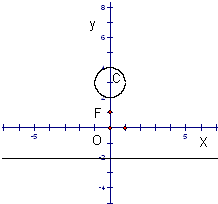 如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1.
如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1.查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分15分)
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5。
(I)求抛物线G的方程;
(II)如图,过抛物线G的焦点的直线依次与抛物线G及圆![]() 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明![]() 为定值;
为定值;
|
查看答案和解析>>
科目:高中数学 来源:2004年广东省深圳市松岗中学高考数学模拟试卷(1)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010年高考数学猜题精粹(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com