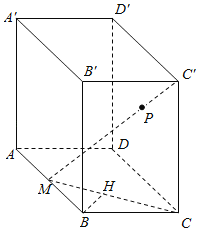
【题目】如图，在长方体
中，
，
，
，M为AB的中点，点P在线段
上，点P到直线
的距离的最小值为________.
【答案】
【解析】
连接MC，运用线面平行的判定定理可得BB'∥平面MCC'，点P到直线BB'的距离的最小值转化为异面直线BB'和直线MC'的距离，即为直线BB'和平面MCC'的距离，即为B到平面MCC'的距离，过B在底面AC内作BH⊥MC，证得BH⊥平面MCC'，求得BH的长即为所求.
解：连接MC，由BB'∥CC'，BB'平面MCC'，CC'平面MCC'，
可得BB'∥平面MCC'，
由点P到直线BB'的距离的最小值为异面直线BB'和直线C'M的距离，
即有直线BB'和平面MCC'的距离即为异面直线BB'和MC'的距离，
也即B到平面MCC'的距离，
过B在底面AC内作BH⊥MC，
由CC'⊥底面AC，可得CC'⊥BH，
即有BH⊥平面MCC'，
由BC＝BM＝1，且BC⊥BA，可得BH＝.
故答案为：.
导学教程高中新课标系列答案
小学课时特训系列答案科目：高中数学 来源： 题型：
【题目】为了解某校学生参加社区服务的情况，采用按性别分层抽样的方法进行调查.已知该校共有学生960人，其中男生560人，从全校学生中抽取了容量为
的样本，得到一周参加社区服务的时间的统计数据好下表：
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
（Ⅰ）求
，；
（Ⅱ）能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关？
（Ⅲ）以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率，现从该校学生中随机调查6名学生，试估计6名学生中一周参加社区服务时间超过1小时的人数.
附：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量
， 
，设函数
，且
的图象过点
和点
.
（Ⅰ）求
的值；
（Ⅱ）将
的图象向左平移
（
）个单位后得到函数
的图象.若
的图象上各最高点到点
的距离的最小值为1，求
的单调增区间.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地举办科技博览会，有
个场馆，现将
个志愿者名额分配给这个场馆，要求每个场馆至少有一个名额且各场馆名额互不相同的分配方法共有（ ）种
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（题文）从某校高一年级随机抽取
名学生，获得了他们日平均睡眠时间（单位：小时）的数据，整理得到数据分组及频数分布表：
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
|
（Ⅰ）求的值．
（Ⅱ）若
，补全表中数据，并绘制频率分布直方图．
（Ⅲ）假设同一组中的每个数据可用该组区间的中点值代替，若上述数据的平均值为
，求
，
的值，并由此估计该校高一学生的日平均睡眠时间不少于
小时的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图
,在矩形
中, 
, 
为
的中点, 
为
的中点.将
沿
折起到
,使得平面
平面
（如图
）.
图1 图2
（Ⅰ）求证: 
；
（Ⅱ）求直线
与平面
所成角的正弦值；
（Ⅲ）在线段
上是否存在点
,使得
平面
?若存在,求出
的值;若不存在,请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】判断下列命题的真假：
（1）
是
的必要条件；
（2）
是
的充要条件；
（3）两个三角形的两组对应角相等是这两个三角形相似的充要条件；
（4）三角形的三条边满足勾股定理是这个三角形为直角三角形的充要条件；
（5）在
中，重心和垂心重合是为等边三角形的必要条件；
（6）如果点
到点
的距离相等，则点一定在线段
的垂直平分线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
