
分析 根据已知首先求出向量的数量积,(1)展开用向量的平方和数量积表示,代入数值计算;
(2)先求其平方,展开,利用向量的平方和数量积计算数值,然后开方求模;
(3)设$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为θ,利用数量积公式得到cosθ的值,从而求向量的夹角.
解答 解:由题意可得|$\overrightarrow{a}$|2=16,|$\overrightarrow{b}$|2=4,且$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos120°=-4,
(1))($\overrightarrow{a}-2\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}-2{\overrightarrow{b}}^{2}-\overrightarrow{a}•\overrightarrow{b}$=16-8+4=12;
(2)|2$\overrightarrow{a}$-$\overrightarrow{b}$|2=4${\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=64+16+4=84,所以|2$\overrightarrow{a}$-$\overrightarrow{b}$|=2$\sqrt{21}$;
(3)设$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为θ,则cosθ=$\frac{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}{|\overrightarrow{a}||\overrightarrow{a}+\overrightarrow{b}|}$=$\frac{{\overrightarrow{a}}^{2}+\overrightarrow{a}•\overrightarrow{b}}{4×\sqrt{16-8+4}}=\frac{16-4}{4×2\sqrt{3}}=\frac{\sqrt{3}}{2}$,又0°≤θ≤180°,所以θ=30°,$\overrightarrow{a}$与$\overrightarrow{a}+\overrightarrow{b}$的夹角为30°.
点评 本题考查了平面向量的数量积运算、模的求法向量的夹角求法;关键是熟练掌握数量积公式,灵活运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 不支持 | 合计 | |
| 中型企业 | 80 | 40 | 120 |
| 小型企业 | 240 | 200 | 440 |
| 合计 | 320 | 240 | 560 |
| P(K2≥k0) | 0.050 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞)上单调递减 | B. | $(\frac{1}{e},+∞)$上单调递减 | C. | $(0,\frac{1}{e})$上单调递减 | D. | (0,+∞)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 非统计专业 | 统计专业 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
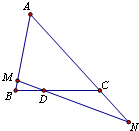 在△ABC中,点D在线段BC上,且满足BD=$\frac{1}{2}$DC,过点D的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AM}$=m$\overrightarrow{AB}$,$\overrightarrow{AN}$=n$\overrightarrow{AC}$,则( )
在△ABC中,点D在线段BC上,且满足BD=$\frac{1}{2}$DC,过点D的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AM}$=m$\overrightarrow{AB}$,$\overrightarrow{AN}$=n$\overrightarrow{AC}$,则( )| A. | m+n是定值,定值为2 | B. | 2m+n是定值,定值为3 | ||
| C. | $\frac{1}{m}$+$\frac{1}{n}$是定值,定值为2 | D. | $\frac{2}{m}$+$\frac{1}{n}$是定值,定值为3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60℃ | B. | 58℃ | C. | 240℃ | D. | 64℃ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com