
【题目】在四棱锥![]() 中,底面
中,底面![]() 为菱形,侧面
为菱形,侧面![]() 为等边三角形,且侧面
为等边三角形,且侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
(Ⅰ)求证: ![]() .
.
(Ⅱ)求证:平面![]() 平面
平面![]() .
.
(Ⅲ)侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ)侧棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.
【解析】试题分析:(1)要证![]() ,只需证明
,只需证明![]() 平面
平面![]() 即可;(2)连结
即可;(2)连结![]() ,因为四边形
,因为四边形![]() 为菱形,所以
为菱形,所以![]() ,因为
,因为![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,且
,且![]() ,由(1)知
,由(1)知![]() 平面
平面![]() ,进而证得
,进而证得![]() 平面
平面![]() ,从而证的平面
,从而证的平面![]() 平面
平面![]() ;(3)设
;(3)设![]() 与
与![]() 的交点分别为
的交点分别为![]() 连结
连结![]() ,因为四边形
,因为四边形![]() 为菱形,
为菱形, ![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,设
,设![]() 为
为![]() 上靠近
上靠近![]() 点三等分点,则
点三等分点,则![]() ,所以
,所以![]() ,进而得到
,进而得到![]() 平面
平面![]() .
.
试题解析:解:(1)因为![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 的中点,
的中点,
所以![]() 又因为平面
又因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
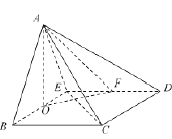
(2)连结![]() ,因为四边形
,因为四边形![]() 为菱形,所以
为菱形,所以![]() ,因为
,因为![]() 分别为
分别为![]() 的中点,
的中点,
所以![]() ,由(1)知
,由(1)知![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
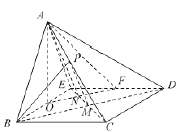
(3)当点![]() 为
为![]() 上的三等分点(靠近
上的三等分点(靠近![]() 点)时,
点)时, ![]() 平面
平面![]() .
.
证明如下:设![]() 与
与![]() 的交点分别为
的交点分别为![]() 连结
连结![]() .因为四边形
.因为四边形![]() 为菱形,
为菱形,
![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,设
,设![]() 为
为![]() 上靠近
上靠近![]() 点三等分点,
点三等分点,
则![]() ,所以
,所以![]() ,因为
,因为![]() 平面
平面![]() 平面
平面
![]() 平面
平面![]() .由于
.由于![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,
, ![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .可见侧棱
.可见侧棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,
,
且![]() .
.


科目:高中数学 来源: 题型:
【题目】有下列说法:
①从投影的角度看,三视图画出的图形都是在平行投影下画出来的图形;
②平行投影的投影线互相平行,中心投影的投影线相交于一点;
③空间几何体在平行投影与中心投影下有不同的表现形式.
其中正确命题的个数为 ( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆心是(4,-1),且过点(5,2)的圆的标准方程是( )
A.(x-4)2+(y+1)2=10
B.(x+4)2+(y-1)2=10
C.(x-4)2+(y+1)2=100
D.(x+4)2+(y-1)2=10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(用数字作答)从5本不同的故事书和4本不同的数学书中选出4本,送给4位同学,每人1本,问:
(1)如果故事书和数学书各选2本,共有多少种不同的送法?
(2)如果故事书甲和数学书乙必须送出,共有多少种不同的送法?
(3)如果选出的4本书中至少有3本故事书,共有多少种不同的送法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为a,E、F、G、H分别为AB、BC、CD、DA的中点.若沿EF、FG、GH、HE将四角折起,试问能折成一个四棱锥吗?为什么?你从中能得到什么结论?对于圆锥有什么类似的结论?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com