
| A. | x1x2<0 | B. | 0<x1x2<1 | C. | x1x2=1 | D. | x1x2>1 |
分析 能够分析出f(x)的零点便是函数y=|lnx|和函数y=($\frac{1}{2}$)x交点的横坐标,从而可画出这两个函数图象,由图象懒虫不等式组,然后求解即可.
解答 解:令f(x)=0,∴|lnx|=($\frac{1}{2}$)x;
∴函数f(x)的零点便是上面方程的解,即是函数y=|lnx|和函数y=($\frac{1}{2}$)x的交点,
画出这两个函数图象如下: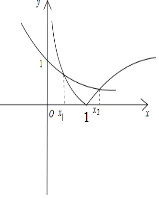
由图看出$\frac{1}{2}$<-lnx1<1,-1<lnx1<0,0<lnx2<$\frac{1}{2}$;
∴-1<lnx1+lnx2<0;
∴-1<lnx1x2<0;
∴0<$\frac{1}{e}$<x1x2<1
故选:B.
点评 考查函数零点的概念,函数零点和方程解的关系,方程f(x)=g(x)的解和函数f(x)与g(x)交点的关系,对数的运算,以及对数函数的单调性.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $(-1,-\frac{7}{8})$ | B. | (0,+∞) | C. | (-∞,0) | D. | $(1,\frac{6}{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
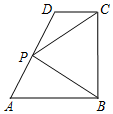 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设$\overrightarrow{AP}=x\overrightarrow{AD}$,$\overrightarrow{PB}•\overrightarrow{PC}=y$,则得到函数y=f(x).
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设$\overrightarrow{AP}=x\overrightarrow{AD}$,$\overrightarrow{PB}•\overrightarrow{PC}=y$,则得到函数y=f(x).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -3 | C. | $\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 0 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=$\frac{π}{3}$,AD=4,AM=2,E是AB的中点
如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=$\frac{π}{3}$,AD=4,AM=2,E是AB的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com