
| A. | (-2,-1) | B. | (-∞,-2)∪(-1,+∞) | C. | $(-\root{3}{{\frac{3}{2}}},-1)$ | D. | $(-∞,-\root{3}{{\frac{3}{2}}})∪(-1,+∞)$ |
分析 求出函数的导数,得到极值点,利用已知条件列出不等式求解即可.
解答 解:f′(x)=x2-(2a+1)x+a(a+1)=(x-a)[x-(a+1)],
f(x)在x=a处取得极大值f(a)=$\frac{1}{3}$a3+$\frac{1}{2}$,
在x=a+1处取得极小值f(a+1)=$\frac{1}{3}$a3+$\frac{1}{3}$,
∴$\frac{1}{3}$a3+$\frac{1}{2}$>0且$\frac{1}{3}$a3+$\frac{1}{3}$<0,解得a$>-\root{2}{\frac{3}{2}}$且a<-1,
可得a∈$(-\root{3}{{\frac{3}{2}}},-1)$.
故选:C.
点评 本题考查函数的导数的应用,函数的极值的应用,考查转化思想以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
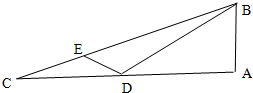 如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=$\frac{1}{2}BD,CE=\frac{1}{4}$EB.∠BDE=120°,CD=3,则BC=$\sqrt{93}$.
如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=$\frac{1}{2}BD,CE=\frac{1}{4}$EB.∠BDE=120°,CD=3,则BC=$\sqrt{93}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{12},0)$ | B. | $(\frac{5π}{12},0)$ | C. | $(-\frac{5π}{12},0)$ | D. | $(\frac{π}{6},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
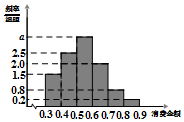 某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )
某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )| A. | 2000 | B. | 4500 | C. | 6000 | D. | 7500 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e2 | B. | e4 | C. | e8 | D. | e16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com