
【题目】函数f(x)=sin(ωx+φ)( ![]() )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点 ![]() 对称
对称
B.关于点 ![]() 对称
对称
C.关于直线 ![]() 对称
对称
D.关于直线 ![]() 对称
对称
【答案】C
【解析】解:由题意可得 ![]() =π,解得ω=2,故函数f(x)=sin(2x+φ),其图象向右平移
=π,解得ω=2,故函数f(x)=sin(2x+φ),其图象向右平移 ![]() 个单位后得到的图象对应的函数为 y=sin[2(x﹣
个单位后得到的图象对应的函数为 y=sin[2(x﹣ ![]() )+φ]=sin(2x﹣
)+φ]=sin(2x﹣ ![]() +φ]是奇函数,故φ=﹣
+φ]是奇函数,故φ=﹣ ![]() ,
,
故 函数f(x)=sin(2x﹣ ![]() ),故当
),故当 ![]() 时,函数f(x)=sin
时,函数f(x)=sin ![]() =1,故函数f(x)=sin(2x﹣
=1,故函数f(x)=sin(2x﹣ ![]() ) 关于直线
) 关于直线 ![]() 对称,
对称,
故选C.
【考点精析】本题主要考查了正弦函数的奇偶性和函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握正弦函数为奇函数;图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】某金匠以黄金为原材料加工一种饰品,经多年的数据统计得知,该金匠平均每加5 个饰品中有4个成品和1个废品,每个成品可获利3万元,每个废品损失1万元,假设该金匠加工每件饰品互不影响,以频率估计概率.
(1)若金金匠加工4个饰品,求其中废品的数量不超过1的概率;
(2)若该金匠加工了 3个饰品,求他所获利润的数学期望.
(两小问的计算结果都用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙丙丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为 ![]() , 有以下结论:
, 有以下结论:
①当x>1时,甲在最前面;
②当x>1时,乙在最前面;
③当0<x<1时,丁在最前面,当x>1时,丁在最后面;
④丙不可能在最前面,也不可能最最后面;
⑤如果它们已知运动下去,最终在最前面的是甲.
其中,正确结论的序号为(把正确结论的序号都填上,多填或少填均不得分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次数学考试中,第22题和第23题为选做题,规定每位考生必须且只须在其中选做一题,现有甲、乙、丙、丁4名考生参加考试,其中甲、乙选做第22题的概率均为![]() ,丙、丁选做第22题的概率均为
,丙、丁选做第22题的概率均为![]() .
.
(Ⅰ)求在甲选做第22题的条件下,恰有两名考生选做同一道题的概率;
(Ⅱ)设这4名考生中选做第22题的学生个数为X,求X的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若奇函数y=f(x)在区间(0,+∞)上是增函数,又f(﹣3)=0,则不等式f(x)<0的解集为( )
A.(﹣3,0)∪(3,+∞)
B.(﹣3,0)∪(0,3)
C.(﹣∞,﹣3)∪(0,3)
D.(﹣∞,﹣3)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于 . 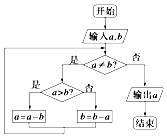
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com