
【题目】(本题满分15分)如图,已知抛物线![]() ,点A
,点A![]() ,
,![]() ,抛物线上的点
,抛物线上的点![]() .过点B作直线AP的垂线,垂足为Q.
.过点B作直线AP的垂线,垂足为Q.

(Ⅰ)求直线AP斜率的取值范围;
(Ⅱ)求![]() 的最大值.
的最大值.
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC. 
(Ⅰ)求BD的长;
(Ⅱ)求sin∠CBD的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用寒假进行社会实践活动,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 | p |
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) | a | 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55) | 15 | 0.3 |

(1)补全频率分布直方图并求n、a、p的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB= ![]() ,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( ) 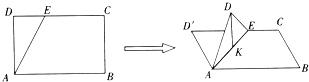
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等边三角形![]() 的边长为4,四边形
的边长为4,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() ,
, ![]() ,
, ![]() 上的点.
上的点.
(Ⅰ)如图①,若![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,证明:
,证明: ![]() 平面
平面![]() ;
;
(Ⅱ)如图②,若![]() ,
, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点,
的中点, ![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用an的信息如图. 
(1)求an;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(I)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(II)求证:![]() 平面
平面![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com