
【题目】在![]() 中,
中,![]() ,若
,若![]() ,则
,则![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
根据题意,由向量线性运算法则可得![]() =
=![]() ,即可得P为△ABC的重心,则有
,即可得P为△ABC的重心,则有![]() +
+![]() +
+![]() =
=![]() ,由正弦定理分析sinB
,由正弦定理分析sinB![]() +2sinA
+2sinA![]() +3sinC
+3sinC![]() =
=![]() 可得b
可得b![]() +2a
+2a![]() +3c
+3c![]() =
=![]() ,由向量减法法则可得b(
,由向量减法法则可得b(![]() ﹣
﹣![]() )+2a
)+2a![]() +3c
+3c![]() =
=![]() ,即b
,即b![]() +(2a﹣b)
+(2a﹣b)![]() +3c
+3c![]() =
=![]() ,由平面向量基本定理可得
,由平面向量基本定理可得![]() ,解可得a=b=3c,由余弦定理计算可得答案.
,解可得a=b=3c,由余弦定理计算可得答案.
:根据题意,如图,在△ABC中,设D为BC的中点,
有![]() +
+![]() =2
=2![]() ,
,
又由![]() =
=![]() (
(![]() +
+![]() ),则
),则![]() =
=![]() ,
,
则P为△ABC的重心,则有![]() +
+![]() +
+![]() =
=![]() ,
,
若sinB![]() +2sinA
+2sinA![]() +3sinC
+3sinC![]() =
=![]() ,则b
,则b![]() +2a
+2a![]() +3c
+3c![]() =
=![]() ,
,
而![]() =
=![]() ﹣
﹣![]() ,
,
则b(![]() ﹣
﹣![]() )+2a
)+2a![]() +3c
+3c![]() =
=![]() ,
,
b![]() +(2a﹣b)
+(2a﹣b)![]() +3c
+3c![]() =
=![]() ,
,
又由![]() +
+![]() +
+![]() =
=![]() ,
,
则有![]() ,解可得a=b=3c,
,解可得a=b=3c,
则cosC=![]() =
=![]() ;
;
故选:D.


科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),M为
为参数),M为![]() 上的动点,P点满足
上的动点,P点满足![]() ,点P的轨迹为曲线
,点P的轨迹为曲线![]() .
.
(I)求![]() 的方程;
的方程;
(II)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为A,与
的异于极点的交点为A,与![]() 的异于极点的交点为B,求|AB|.
的异于极点的交点为B,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问50名性别不同的大学生是否爱好某项运动,得到如下的列联表,由![]() 得
得![]()
参照附表,得到的正确结论是
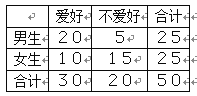

A. 有99.5%以上的把握认为“爱好该项运动与性别有关”
B. 有99.5%以上的把握认为“爱好该项运动与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另外15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另外30人比较粗心.
(I)试根据上述数据完成![]() 列联表:
列联表:

(II)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解四川省各景点在大众中的熟知度,随机对![]() 岁的人群抽样了
岁的人群抽样了![]() 人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.
人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.

组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
第 |
| | |
第 |
| | |
第 |
| | |
第 |
| | |
第 |
| | |
(1)分别求出![]() 的值;
的值;
(2)从第![]() ,
,![]() ,
,![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() ,
,![]() ,
,![]() 组每组各抽取多少人?
组每组各抽取多少人?
(3)通过直方图求出年龄的众数,平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内的两点P,Q满足条件:①P,Q都在函数![]() 的图像上;②P,Q关于原点对称,则称P,Q是函数
的图像上;②P,Q关于原点对称,则称P,Q是函数![]() 的一对“友好点对”(点对P,Q与Q,P看作同一对“友好点对”).已知函数
的一对“友好点对”(点对P,Q与Q,P看作同一对“友好点对”).已知函数 若此函数的“友好点对”有且只有一对,则a的取值范围是( )
若此函数的“友好点对”有且只有一对,则a的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生从全校学生中随机选取![]() 名统计他们的鞋码大小,得到如下数据:
名统计他们的鞋码大小,得到如下数据:
鞋码 |
|
|
|
|
|
|
|
|
|
| 合计 |
男生 |
|
|
|
|
|
|
|
|
| ||
女生 |
|
|
|
|
|
|
|
|
|
以各性别各鞋码出现的频率为概率.
(![]() )从该校随机挑选一名学生,求他(她)的鞋码为奇数的概率.
)从该校随机挑选一名学生,求他(她)的鞋码为奇数的概率.
(![]() )为了解该校学生考试作弊的情况,从该校随机挑选
)为了解该校学生考试作弊的情况,从该校随机挑选![]() 名学生进行抽样调查.每位学生从装有除颜色外无差别的
名学生进行抽样调查.每位学生从装有除颜色外无差别的![]() 个红球和
个红球和![]() 个白球的口袋中,随机摸出两个球,若同色,则如实回答其鞋码是否为奇数;若不同色,则如实回答是否曾在考试中作弊.这里的回答,是指在纸上写下“是”或“否”.若调查人员回收到
个白球的口袋中,随机摸出两个球,若同色,则如实回答其鞋码是否为奇数;若不同色,则如实回答是否曾在考试中作弊.这里的回答,是指在纸上写下“是”或“否”.若调查人员回收到![]() 张“是”的小纸条,试估计该校学生在考试中曾有作弊行为的概率.
张“是”的小纸条,试估计该校学生在考试中曾有作弊行为的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com