
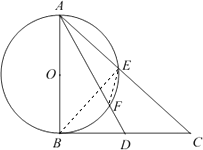
【题目】如图,在直角△ABC中,AB⊥BC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F. 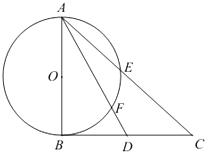
(1)证明:C,E,F,D四点共圆;
(2)若D为BC的中点,且AF=3,FD=1,求AE的长.
【答案】
(1)证明:连结EF,BE,则∠ABE=∠AFE,因为AB是⊙O是直径,
所以,AE⊥BE,又因为AB⊥BC,∠ABE=∠C,
所以∠AFE=∠C,即∠EFD+∠C=180°,
∴C,E,F,D四点共圆.
(2)解:因为AB⊥BC,AB是直径,
所以,BC是圆的切线,DB2=DFDA=4,即BD=2,
所以,AB= ![]() =2
=2 ![]() ,
,
因为D为BC的中点,所以BC=4,AC= ![]() =2
=2 ![]() ,
,
因为C、E、F、D四点共圆,所以AEAC=AFAD,
即2 ![]() AE=12,即AE=
AE=12,即AE= ![]()
【解析】(1)连结EF,BE,说明AB是⊙O是直径,推出∠ABE=∠C,然后证明C,E,F,D四点共圆.(2)利用切割线定理求解BD,利用C、E、F、D四点共圆,得到AEAC=AFAD,然后求解AE.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】下列四种说法正确的是( )
①函数f(x)的定义域是R,则“x∈R,f(x+1)>f(x)”是“函数f(x)为增函数”的充要条件
②命题“x∈R,( ![]() )x>0”的否定是“x∈R,(
)x>0”的否定是“x∈R,( ![]() )x≤0”
)x≤0”
③命题“若x=2,则x2﹣3x+2=0”的逆否命题是“若x2﹣3x+2≠0,则x≠2”
④p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数.则p∧q为真命题.
A.①②③④
B.①③
C.①③④
D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为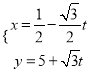 (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系.
轴的正半轴为极轴建立坐标系.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)射线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,能推断这个几何体可能是三棱台的是( ) 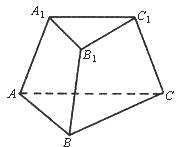
A.A1B1=2,AB=3,B1C1=3,BC=4
B.A1Bl=1,AB=2,BlCl=1.5,BC=3,A1C1=2,AC=3
C.AlBl=1,AB=2,B1Cl=1.5,BC=3,AlCl=2,AC=4
D.AB=A1B1 , BC=B1C1 , CA=C1A1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(4)与f(8)的值;
(2)解不等式f(x)﹣f(x﹣2)>3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是( )
A.(x-2)2+(y-1)2=1
B.(x-2)2+(y-3)2=1
C.(x-3)2+(y-2)2=1
D.(x-3)2+(y-1)2=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查者100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图,若日销量不低于50件,则称当日为“畅销日”.
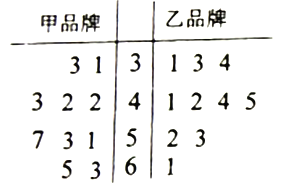
(1)现从甲品牌日销量大于40且小于60的样本中任取两天,求这两天都是“畅销日”的概率;
(2)用抽取的样本估计这100天的销售情况,请完成这两种品牌100天销量的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为品牌与“畅销日”天数有关.
的把握认为品牌与“畅销日”天数有关.
附: 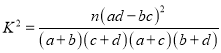 (其中
(其中![]() )
)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
畅销日天数 | 非畅销日天数 | 合计 | |
甲品牌 | |||
乙品牌 | |||
合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com