
| 2(1-λ) |
| 2(1+λ) |
| 2 |
| 1+λ |
| 2(1-λ) |
| 2(1+λ) |
| 2λ |
| 1+λ |


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
| A、若m∥n,n?α则 m∥α |
| B、若m?α,α⊥β,则m⊥β |
| C、若m∥n,m⊥α,则n⊥α |
| D、若m⊥n,m?α,n?β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<
如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<| π |
| 2 |
| 3 |
| 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:
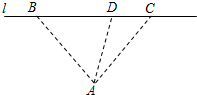 某供货商拟从码头A发货至其对岸l的两个商场B,C处,通常货物先由A处船运至BC之间的中转站D,再利用车辆转运.如图,码头A与两商场B,C的距离相等,两商场间的距离为20千米,且∠BAC=
某供货商拟从码头A发货至其对岸l的两个商场B,C处,通常货物先由A处船运至BC之间的中转站D,再利用车辆转运.如图,码头A与两商场B,C的距离相等,两商场间的距离为20千米,且∠BAC=| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
| C、若p∧q为假命题,则p,q均为假命题 |
| D、若关于x的不等式ax2+ax-2<0恒成立,则-8<a<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| a2-a1 |
| 1 |
| a3-a2 |
| 1 |
| an+1-an |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com