
【题目】已知函数f(x)=|cosx|sinx,给出下列五个说法:
①f( ![]() π)=﹣
π)=﹣ ![]() ;
;
②若|f(x1)|=|f(x2)|,则x1=x2+kπ(k∈Z);
③f(x)在区间[﹣ ![]() ,
, ![]() ]上单调递增;
]上单调递增;
④函数f(x)的周期为π.
⑤f(x)的图象关于点( ![]() ,0)成中心对称.
,0)成中心对称.
其中正确说法的序号是 .
【答案】①③
【解析】解:由题意函数f(x)=|cosx|sinx= 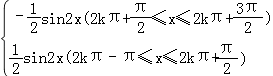 (k∈Z);
(k∈Z);
对于①:f( ![]() π)=|cos
π)=|cos ![]() |sin
|sin ![]() =)=|cos(
=)=|cos( ![]() )|sin(27π
)|sin(27π ![]() )=
)= ![]() =﹣
=﹣ ![]() ;所以①对
;所以①对
对于②:若|f(x1)|=|f(x2)|,当x2= ![]() ,x1=
,x1= ![]() 时,成立,则x1=x2+
时,成立,则x1=x2+ ![]() ,所以②不对
,所以②不对
对于③f(x)在区间[﹣ ![]() ,
, ![]() ]上时,f(x)=
]上时,f(x)= ![]() sin2x,可得2x∈[-
sin2x,可得2x∈[- ![]() ,
, ![]() ],x∈[﹣
],x∈[﹣ ![]() ,
, ![]() ]上是单调递增;所以③对.
]上是单调递增;所以③对.
对于④:函数f(x)=|cosx|sinx,则f(x+π)=|cos(x+π)|sin(x+π)=﹣(|cosx|sinx)=﹣f(x),可得函数f(x)的周期不是π.所以④不对.
对于⑤:由于f( ![]() )=|cos(x+
)=|cos(x+ ![]() )|sin(x+
)|sin(x+ ![]() )=cosx|sinx|,f(
)=cosx|sinx|,f( ![]() )=|cos(﹣x+
)=|cos(﹣x+ ![]() )|sin(﹣x+
)|sin(﹣x+ ![]() )=cosx|sinx|
)=cosx|sinx|
则:f( ![]() )=f(
)=f( ![]() )图象关于x=
)图象关于x= ![]() 对称.所以⑤不对.
对称.所以⑤不对.
综上所得:①③正确,②④⑤不对.
所以答案是:①③.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=![]() AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.
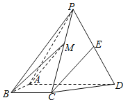
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行某项对抗性游戏,采用“七局四胜”制,即先赢四局者为胜,若甲、乙两人水平相当,且已知甲先赢了前两局.
![]() Ⅰ
Ⅰ![]() 求乙取胜的概率;
求乙取胜的概率;
![]() Ⅱ
Ⅱ![]() 记比赛局数为X,求X的分布列及数学期望
记比赛局数为X,求X的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校青年职工、中年职工、老年职工的人数之比为7:5:3,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本 .若样本中的青年职工为14人,则样本容量为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣10|+|x﹣20|,且满足f(x)<10a+10(a∈R)的解集不是空集.
(Ⅰ)求实数a的取值集合A
(Ⅱ)若b∈A,a≠b,求证aabb>abba .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京市环境保护监测中心每月向公众公布北京市各区域的空气质量状况![]() 年1月份各区域的
年1月份各区域的![]() 浓度情况如表:
浓度情况如表:
各区域1月份![]() 浓度
浓度![]() 单位:微克
单位:微克![]() 立方米
立方米![]() 表
表
区域 |
| 区域 |
| 区域 |
|
怀柔 | 27 | 海淀 | 34 | 平谷 | 40 |
密云 | 31 | 延庆 | 35 | 丰台 | 42 |
门头沟 | 32 | 西城 | 35 | 大兴 | 46 |
顺义 | 32 | 东城 | 36 | 开发区 | 46 |
昌平 | 32 | 石景山 | 37 | 房山 | 47 |
朝阳 | 34 | 通州 | 39 |
从上述表格随机选择一个区域,其2018年1月份![]() 的浓度小于36微克
的浓度小于36微克![]() 立方米的概率是
立方米的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|ax﹣2|.
(1)若关于x的不等式f(x)<3的解集为(﹣ ![]() ,
, ![]() ),求a的值;
),求a的值;
(2)f(x)+f(﹣x)≥a对于任意x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2﹣x .
(1)求方程f(x)= ![]() 的根;
的根;
(2)求证:f(x)在[0,+∞)上是增函数;
(3)若对于任意x∈[0,+∞),不等式f(2x)≥f(x)﹣m恒成立,求实数m的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com