
分析 本题考查的知识点是几何概型的意义,关键是要找出蚂蚁距离三角形的三个顶点的距离不超过1时对应线段的长度,并将它同三角形的周长代入几何概型的计算公式,进行求解.
解答 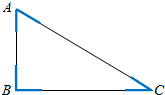 解:如下图所示,当蚂蚁位于图中蓝色线段上时,距离三角形的三个顶点的距离不超过1,
解:如下图所示,当蚂蚁位于图中蓝色线段上时,距离三角形的三个顶点的距离不超过1,
由已知易得:蓝色线段的长度和为:6
三角形的周长为:6+8+10=24,
故P=$\frac{6}{24}$=$\frac{1}{4}$
故答案为:$\frac{1}{4}$
点评 几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=$\frac{N(A)}{N}$求解.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{7}}{7}$ | B. | $\frac{\sqrt{21}}{7}$ | C. | $\frac{\sqrt{35}}{7}$ | D. | $\frac{2\sqrt{21}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | 频率分布直方图 |
| 第1组 | [15,25) | 5 | 0.5 | 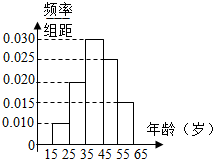 |
| 第2组 | [25,35) | a | 0.9 | |
| 第3组 | [35,45) | 27 | x | |
| 第4组 | [45,55) | 9 | 0.36 | |
| 第5组 | [55,65] | 3 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,-1) | B. | (4,1) | C. | (0,-9) | D. | (-2,-5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}(\overrightarrow a-\overrightarrow b)$ | B. | $\frac{1}{2}(\overrightarrow a+\overrightarrow b)$ | C. | $\frac{1}{2}(\overrightarrow b-\overrightarrow a)$ | D. | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com