
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益
,乙城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元)。
(单位:万元)。
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
【答案】(1)43.5(2)当甲城市投资72万元,乙城市投资48万元时,总收益最大,且最大收益为44万元
【解析】试题分析:(1)把![]() 代入
代入![]() 可得总收益
可得总收益
(2)设甲城市投资![]() 万元,则乙城市投资
万元,则乙城市投资![]() 万元,可得总收益为
万元,可得总收益为![]() ,由
,由![]() 得到满足题意的x的范围,通过二配方得到关于
得到满足题意的x的范围,通过二配方得到关于![]() 函数,可得最值
函数,可得最值
试题解析:(1)当![]() 时,此时甲城市投资50万元,乙城市投资70万元
时,此时甲城市投资50万元,乙城市投资70万元
所以总收益 ![]() =43.5(万元)
=43.5(万元)
(2)由题知,甲城市投资![]() 万元,乙城市投资
万元,乙城市投资![]() 万元
万元
所以![]()
![]()
依题意得![]() ,解得
,解得![]()
故![]()
![]()
令![]() ,则
,则![]()
所以![]()
当![]() ,即
,即![]() 万元时,
万元时, ![]() 的最大值为44万元
的最大值为44万元
所以当甲城市投资72万元,乙城市投资48万元时,总收益最大,且最大收益为44万元
点晴:解决函数模型应用的解答题,要注意以下几点:①读懂实际背景,将实际问题转化为函数模型.②对题目中自变量的范围要求准确.③在求解的过程中结合定义域求出函数的最值.另外需要熟练掌握求解方程、不等式、函数最值的方法,才能快速正确地求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别是椭圆
分别是椭圆![]()
![]()
![]() 的左、右焦点,点
的左、右焦点,点![]() 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,其中
,其中![]() 为坐标原点,判断
为坐标原点,判断![]() 到直线
到直线![]() 的距离是否为定值?若是,求出该定值;若不是,请说明理由.
的距离是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表:
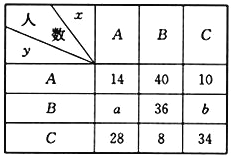
若抽取学生![]() 人,成绩分为
人,成绩分为![]() (优秀),
(优秀),![]() (良好),
(良好),![]() (及格)三个等次,设
(及格)三个等次,设![]() 分别表示数学成绩与地理成绩,例如:表中地理成绩为
分别表示数学成绩与地理成绩,例如:表中地理成绩为![]() 等级的共有
等级的共有![]() (人),数学成绩为
(人),数学成绩为![]() 等级且地理成绩为
等级且地理成绩为![]() 等级的共有8人.已知
等级的共有8人.已知![]() 与
与![]() 均为
均为![]() 等级的概率是
等级的概率是![]() .
.
(1)设在该样本中,数学成绩的优秀率是![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,
,![]() ,求数学成绩为
,求数学成绩为![]() 等级的人数比
等级的人数比![]() 等级的人数多的概率.
等级的人数多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在函数![]() (
(![]() 为常数),使得对函数
为常数),使得对函数![]() 定义域内任意
定义域内任意![]() 都有
都有![]() 成立,那么称
成立,那么称![]() 为函数
为函数![]() 的一个“线性覆盖函数”.给出如下四个结论:
的一个“线性覆盖函数”.给出如下四个结论:
①函数![]() 存在“线性覆盖函数”;
存在“线性覆盖函数”;
②对于给定的函数![]() ,其“线性覆盖函数”可能不存在,也可能有无数个;
,其“线性覆盖函数”可能不存在,也可能有无数个;
③![]() 为函数
为函数![]() 的一个“线性覆盖函数”;
的一个“线性覆盖函数”;
④若![]() 为函数
为函数![]() 的一个“线性覆盖函数”,则
的一个“线性覆盖函数”,则![]()
其中所有正确结论的序号是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos 2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com