
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)茎叶图如下,乙发挥比较稳定,总体得分情况比甲好;(2)乙.
解析试题分析:(1)画茎叶图时分出茎和叶,根据所给数据,可以以十位数字为茎,个位数字为叶;获得的信息可从茎叶图中数据的分布情况及数字特征如中位数加以说明;(2)根据数据可算出平均数,中位数,方差等数字特征,可知两者平均数相等,乙的方差较小,说时乙发挥稳定,且乙的中位数较大,可选择乙参赛.
试题解析:(1)画茎叶图,其中中间数为数据的十位数,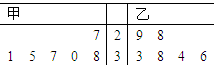
从这个茎叶图上可以看出,甲、乙的得分情况都是分布均匀的,只是乙更好一些;乙的中位数是35,甲的中位数是33,因此乙发挥比较稳定,总体得分情况比甲好;
(2):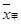 =33,
=33,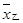 =33,s甲=3.96,s乙=3.56,甲的中位数是33,乙的中位数是35,综合比较选乙参加比赛较为合适.
=33,s甲=3.96,s乙=3.56,甲的中位数是33,乙的中位数是35,综合比较选乙参加比赛较为合适.
考点:茎叶图的画法,数据的数字特征的理解与应用,注意数据方差的计算公式,方差小波动小,数据越稳定,方差大波动大,数据越不稳定。


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如下图所示.该同学为这个开学季购进了160盒该产品,以X(单位:盒,100≤X≤200)表示这个开学季内的市场需求量,Y(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量X的平均数和众数;
(2)将Y表示为X的函数;
(3)根据直方图估计利润不少于4800元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
随机抽取某中学甲班10名同学,他们的身高(单位:cm)数据是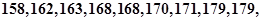
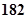 ;乙班10名同学,他们的身高(单位:cm)数据是
;乙班10名同学,他们的身高(单位:cm)数据是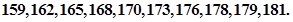
(1)画出甲、乙两班的茎叶图,并说明茎叶图有什么优点和缺点?
(2)根据茎叶图判断哪个班的平均身高较高(不必计算).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:请观察图形,求解下列问题:
(1)79.5~89.5这一组的频率、频数分别是多少?
(2)估计这次环保知识竞赛的及格率(60分及以上为及格)和平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某单位有50名职工,现要从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组,按各组内抽取的编号依次增加5进行系统抽样.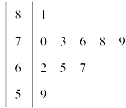
(1)若第5组抽出的号码为22,写出所有被抽出职工的号码;
(2)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的方差;
(3)在(2)的条件下,从这10名职工中随机抽取两名体重不轻于73公斤(≥73公斤)的职工,求体重为76公斤的职工被抽取到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年11月,青岛发生输油管道爆炸事故造成胶州湾局部污染.国家海洋局用分层抽样的方法从国家环保专家、海洋生物专家、油气专家三类专家库中抽取若干人组成研究小组赴泄油海域工作,有关数据见表1(单位:人)
海洋生物专家为了检测该地受污染后对海洋动物身体健康的影响,随机选取了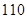 只海豚进行了检测,并将有关数据整理为不完整的
只海豚进行了检测,并将有关数据整理为不完整的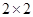 列联表,如表2.
列联表,如表2.
(1)求研究小组的总人数;
(2)写出表2中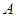 、
、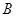 、
、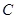 、
、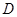 、
、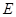 的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
(3)若从研究小组的环保专家和海洋生物专家中随机选 人撰写研究报告,求其中恰好有
人撰写研究报告,求其中恰好有 人为环保专家的概率.
人为环保专家的概率.
附:①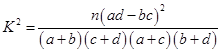 ,其中
,其中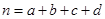 .
.
②
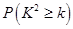 | 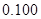 | 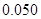 | 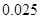 | 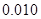 | 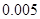 | 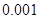 |
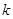 | 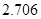 | 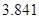 | 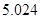 | 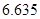 |  | 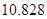 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为迎接6月6日的“全国爱眼日”,某高中学生会从全体学生中随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶),如图,若视力测试结果不低于5.0,则称为“好视力”.
(1)写出这组数据的众数和中位数;
(2)从这16人中随机选取3人,求至少有2人是“好视力”的概率;
(3)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记X表示抽到“好视力”学生的人数,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com