
【题目】已知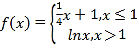 ,则方程
,则方程![]() 恰有2个不同的实根,实数
恰有2个不同的实根,实数![]() 取值范围__________________.
取值范围__________________.
【答案】![]()
【解析】
将问题转化为当直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 个交点时,求实数
个交点时,求实数![]() 的取值范围,并作出函数
的取值范围,并作出函数![]() 的图象,考查当直线
的图象,考查当直线![]() 与曲线
与曲线![]() 相切以及直线
相切以及直线![]() 与直线
与直线![]() 平行这两种临界位置情况,结合斜率的变化得出实数
平行这两种临界位置情况,结合斜率的变化得出实数![]() 的取值范围。
的取值范围。
问题等价于当直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 个交点时,求实数
个交点时,求实数![]() 的取值范围。
的取值范围。
作出函数![]() 的图象如下图所示:
的图象如下图所示:
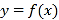
先考虑直线![]() 与曲线
与曲线![]() 相切时,
相切时,![]() 的取值,
的取值,
设切点为![]() ,对函数
,对函数![]() 求导得
求导得![]() ,切线方程为
,切线方程为![]() ,
,
即![]() ,则有
,则有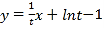 ,解得
,解得![]() .
.
由图象可知,当![]() 时,直线
时,直线![]() 与函数
与函数![]() 在
在![]() 上的图象没有公共点,在
上的图象没有公共点,在![]() 有一个公共点,不合乎题意;
有一个公共点,不合乎题意;
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 在
在![]() 上的图象没有公共点,在
上的图象没有公共点,在![]() 有两个公共点,合乎题意;
有两个公共点,合乎题意;
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 在
在![]() 上的图象只有一个公共点,在
上的图象只有一个公共点,在![]() 有两个公共点,不合乎题意;
有两个公共点,不合乎题意;
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 在
在![]() 上的图象只有一个公共点,在
上的图象只有一个公共点,在![]() 没有公共点,不合乎题意.
没有公共点,不合乎题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() ,故答案为:
,故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C对应的边长分别为a,b,c,向量m=(sinB,1﹣cosB)与向量n=(2,0)的夹角θ的余弦值为![]() .
.
(1)求角B的大小;
(2)若b=![]() ,求a+c的取值范围.
,求a+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 恒成立,则称
恒成立,则称![]() 为
为![]() 的一个上界函数,当(1)中的
的一个上界函数,当(1)中的![]() 为函数
为函数![]() 的一个上界函数时,求
的一个上界函数时,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,对(1)中的
时,对(1)中的![]() ,讨论
,讨论![]() 在区间
在区间![]() 上极值点的个数.
上极值点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】体育测试成绩分为四个等级:优、良、中、不及格.某班50名学生参加测试结果如下:
等级 | 优(86~100分) | 良(75~85分) | 中(60~74分) | 不及格(1~59分) |
人数 | 5 | 21 | 22 | 2 |
(1)估计该班学生体育测试的平均成绩;
(2)从该班任意抽取1名学生,求这名学生的测试成绩为“优”或“良”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿基米德(公元前287年—公元前212年),伟大的古希腊哲学家、数学家和物理学家,他死后的墓碑上刻着一个“圆柱容球”的立体几何图形,为纪念他发现“圆柱内切球的体积是圆柱体积的![]() ,且球的表面积也是圆柱表面积的
,且球的表面积也是圆柱表面积的![]() ”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为
”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为![]() ,则该圆柱的内切球体积为( )
,则该圆柱的内切球体积为( )
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com