
【题目】已知函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)若对于任意的![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(I)当![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间;当
,无单调递减区间;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() ;(II)
;(II)![]()
【解析】
(Ⅰ)求出![]() ,分两种情况讨论,在定义域内,分别令
,分两种情况讨论,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(Ⅱ)对
的减区间;(Ⅱ)对![]() 分四种情况讨论,分别利用导数求出函数
分四种情况讨论,分别利用导数求出函数![]() 最小值的表达式,令
最小值的表达式,令![]() 最小值不小于零,即可筛选出符合题意的
最小值不小于零,即可筛选出符合题意的![]() 的取值范围.
的取值范围.
(Ⅰ)![]() 的定义域为
的定义域为![]() .
.
![]()
![]() .
.
(1)当![]() 时,
时,![]() 恒成立,
恒成立,![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间;
,无单调递减区间;
(2)当![]() 时,由
时,由![]() 解得
解得![]() ,由
,由![]() 解得
解得![]() .
.
∴![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() .
.
(Ⅱ)①当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 恒成立,符合题意.
恒成立,符合题意.
②当![]() 时,由(Ⅰ)知,
时,由(Ⅰ)知,![]() 在
在![]() 、
、![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(i)若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∴对任意的实数![]() ,
,![]() 恒成立,只需
恒成立,只需![]() ,且
,且![]() .
.
而当![]() 时,
时,
![]() 且
且![]() 成立.
成立.
∴![]() 符合题意.
符合题意.
(ii)若![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∴对任意的实数![]() ,
,![]() 恒成立,只需
恒成立,只需![]() 即可,
即可,
此时![]() 成立,
成立,
∴![]() 符合题意.
符合题意.
(iii)若![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
∴对任意的实数![]() ,
,![]() 恒成立,只需
恒成立,只需![]() ,
,
即![]() ,
,
∴![]() 符合题意.
符合题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴非负半轴上,点
轴非负半轴上,点![]() 满足:
满足:![]()
(1)当点![]() 在
在![]() 轴上移动时,求动点
轴上移动时,求动点![]() 的轨迹C的方程;
的轨迹C的方程;
(2)设![]() 为曲线C上一点,直线
为曲线C上一点,直线![]() 过点
过点![]() 且与曲线C在点
且与曲线C在点![]() 处的切线垂直,
处的切线垂直,![]() 与C的另一个交点为
与C的另一个交点为![]() ,若以线段
,若以线段![]() 为直径的圆经过原点,求直线
为直径的圆经过原点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l:x﹣y+4=0和圆O:x2+y2=4,P是直线l上一点,过点P作圆C的两条切线,切点分别为M,N.
(1)若PM⊥PN,求点P坐标;
(2)若圆O上存在点A,B,使得∠APB=60°,求点P的横坐标的取值范围;
(3)设线段MN的中点为Q,l与x轴的交点为T,求线段TQ长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国中医学的发展,药用昆虫的使用相应愈来愈多.每年春暖以后至寒冬前,是昆虫大量活动与繁殖季节,易于采集各种药用昆虫.已知一只药用昆虫的产卵数![]() 与一定范围内的温度
与一定范围内的温度![]() 有关,于是科研人员在3月份的31天中随机挑选了5天进行研究,现收集了该种药用昆虫的5组观测数据如下表:
有关,于是科研人员在3月份的31天中随机挑选了5天进行研究,现收集了该种药用昆虫的5组观测数据如下表:
日期 | 2日 | 7日 | 15日 | 22日 | 30日 |
温度 | 10 | 11 | 13 | 12 | 8 |
产卵数 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记这两天药用昆虫的产卵分别为![]() ,
,![]() ,求事件“
,求事件“![]() ,
,![]() 均不小于25”的概率;
均不小于25”的概率;
(2)科研人员确定的研究方案是:先从这五组数据中任选2组,用剩下的3组数据建立![]() 关于
关于![]() 的线性回归方程,再对被选取的2组数据进行检验.
的线性回归方程,再对被选取的2组数据进行检验.
(ⅰ)若选取的是3月2日与30日的两组数据,请根据3月7日、15日和22日这三天的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(ⅱ)若由线性回归方程得到的估计数据与选出的检验数据的误差均不超过2个,则认为得到的线性回归方程是可靠的,试问(ⅰ)中所得的线性回归方程是否可靠?
附:回归直线的斜率和截距的最小二乘估计公式分别为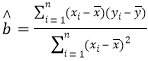 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,设数列{bn}的前n项和为Sn,且2bn=b1(1+Sn),bn≠0,又a2b2=4,a7+b3=11.
(1)求{an}和{bn}的通项公式;
(2)令cn=anbn(n∈N*),求{cn}的前n项和Tn
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,其中
,其中![]() ,连接
,连接![]() ,延长
,延长![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 时,求二面角
时,求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A. 若命题![]() ,
,![]() ,则命题
,则命题![]() ,
,![]()
B. “![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
C. “若![]() ,则
,则![]() 、
、![]() 中至少有一个不小于
中至少有一个不小于![]() ”的逆否命题是真命题
”的逆否命题是真命题
D. ![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com