
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
【答案】投资人用4万元投资甲项目、6万元投资乙项目,才能在确保亏损不超过1.8 万元的前提下,使可能的盈利最大
【解析】试题分析:(1)含有实际背景的线性规划问题其解题关键是找到制约求解目标的两个变量,用这两个变量建立可行域和目标函数,解题时要注意题目中的各种制约的关系,列出全面的制约条件和正确的目标函数;(2)平面区域的画法:线定界、点定线(注意实虚线);(3)求最值:求二元一次函数![]() 的最值,将函数
的最值,将函数![]() 转化为直线的点斜式
转化为直线的点斜式![]() ,通过求直线的截距
,通过求直线的截距![]() 的最值间接求出
的最值间接求出![]() 的最值,最优解在顶点或边界取得.
的最值,最优解在顶点或边界取得.
试题解析:解:设分别向甲、乙两组项目投资![]() 万元,
万元,![]() 万元,利润为
万元,利润为![]() 万元
万元
由题意知
目标函数![]() 作出可行域
作出可行域
作出可行域
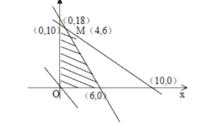
作直线![]() ,并作平行直线
,并作平行直线![]() 的一组直线
的一组直线![]()
![]() ,与可行域相交,其中有一条直线经过可行域上的点
,与可行域相交,其中有一条直线经过可行域上的点![]() 点,且与直线
点,且与直线![]() 的距离
的距离
最大,这里![]() 是直线
是直线![]() 和
和![]()
解方程组![]() ,解得
,解得![]()
此时![]() (万元)
(万元)![]()
![]() 当
当![]() 时
时![]() 最大
最大
答:投资人投资甲项目4万元,乙项目6万元,获得利润最大


科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是(﹣1,1)上的偶函数,且在区间(﹣1,0)上是单调递增的,A,B,C是锐角三角形△ABC的三个内角,则下列不等式中一定成立的是( )
A.f(sinA)>f(sinB)
B.f(sinA)>f(cosB)
C.f(cosC)>f(sinB)
D.f(sinC)>f(cosB)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f′(x)=2+sinx,且f(0)=﹣1,数列{an}是以 ![]() 为公差的等差数列,若f(a2)+f(a3)+f(a4)=3π,则
为公差的等差数列,若f(a2)+f(a3)+f(a4)=3π,则 ![]() =( )
=( )
A.2016
B.2015
C.2014
D.2013
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]()
(1)求椭圆C的方程;
(2)设过点M(2,0)的直线l与椭圆C相交于A,B两点,F1为椭圆的左焦点.
①若B点关于x轴的对称点是N,证明:直线AN恒过一定点;
②试求椭圆C上是否存在点P,使F1APB为平行四边形?若存在,求出F1APB的面积,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示程序框图是用“二分法”求方程![]() 的近似解的算法,有下列判断:
的近似解的算法,有下列判断:
①若![]() 则输出的值在
则输出的值在![]() 之间;
之间;
②若![]() 则程序执行完毕将没有值输出;
则程序执行完毕将没有值输出;
③若![]() 则程序框图最下面的判断框刚好执行8次程序就结束.
则程序框图最下面的判断框刚好执行8次程序就结束.
其中正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报说,在今后的三天中,每一天下雨的概率均为![]() ,某同学用随机模拟的方法确定这三天中恰有两天下雨的概率,该同学利用计算器可以产生0到9之间的取整数值的随机数,他用1,4,7表示下雨,用0,2,3,5,6,8,9表示不下雨。实验得出如下20组随机数:
,某同学用随机模拟的方法确定这三天中恰有两天下雨的概率,该同学利用计算器可以产生0到9之间的取整数值的随机数,他用1,4,7表示下雨,用0,2,3,5,6,8,9表示不下雨。实验得出如下20组随机数:
245,368,590,126,217,895,560,061,378,902
542,751,245,602,156,035,682,148,357,438
请根据该同学实验的数据确定这三天中恰有两天下雨的概率为 __________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组中的两个集合相等的有( )
①P={x|x=2n,n∈Z},Q={x|x=2(n-1),n∈Z};
②P={x|x=2n-1,n∈N*},Q={x|x=2n+1,n∈N*};
③P={x|x2-x=0},Q=![]() .
.
A. ①②③ B. ①③
C. ②③ D. ①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com