[题目]若函数同时满足:⑴对于定义域上的任意.恒有, ⑵对于定义域上的任意.当时.恒有.则称函数为“理想函数 .给出下列四个函数中: ①.②. ③.④.能被称为“理想函数的有 . 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】若函数同时满足：⑴对于定义域上的任意，恒有； ⑵对于定义域上的任意，当时，恒有，则称函数为“理想函数”.给出下列四个函数中： ①，②， ③，④，能被称为“理想函数”的有_____________（填相应的序号）.

【答案】④.

【解析】

根据条件为定义域上的奇函数且是减函数，对给出的四个函数进行逐一判断即可.

由题意，性质⑴反映了函数为定义域上的奇函数.

性质⑵反映了函数为定义域上的单调递减函数.

①中，函数为定义域上的奇函数，但不是定义域上的单调减函数，所以①不正确.

②中，函数为定义域上的非奇非偶函数，所以②不正确.

③中，函数的定义域为，为单调增函数，所以③不正确.

④中，函数的图象如图所示，显然此函数为奇函数且在定义域R上为减函数，所以为理想函数，所以④正确.

故答案为：④．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知奇函数的定义域为[-1,1]，当时，。

（1）求函数在上的值域；

（2）若时，函数的最小值为-2，求实数λ的值。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数，．

（1）若在处取得极值，求的值；

（2）设，试讨论函数的单调性；

（3）当时，若存在正实数满足，求证：．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设是由个有序实数构成的一个数组，记作：.其中称为数组的“元”，为的下标.如果数组中的每个“元”都来自数组中不同下标的“元”则称为的子数组.定义两个数组，的关系数为.

（1）若，，设是的含有两个“元”的子数组，求的最大值及此时的数组；

（2）若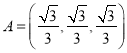，，且，为的含有三个“元”的子数组，求的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某险种的基本保费为（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其

上年度出险次数的关联如下：

上年度出险次数	0	1	2	3	4
保费

随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：

出险次数	0	1	2	3	4
频数	60	50	30	30	20	10

（1）记A为事件：“一续保人本年度的保费不高于基本保费”.求的估计值；

（2）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160％”.求的估计值；

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”，彰显出中国式创新的强劲活力.某移动支付公司从我市移动支付用户中随机抽取100名进行调查，得到如下数据：

每周移动支付次数	1次	2次	3次	4次	5次	6次及以上
男	10	8	7	3	2	15
女	5	4	6	4	6	30
合计	15	12	13	7	8	45

（1）把每周使用移动支付6次及6次以上的用户称为“移动支付达人”，按分层抽样的方法，在我市所有“移动支付达人”中，随机抽取6名用户

求抽取的6名用户中，男女用户各多少人；

② 从这6名用户中抽取2人，求既有男“移动支付达人”又有女“移动支付达人”的概率.

（2）把每周使用移动支付超过3次的用户称为“移动支付活跃用户”，填写下表，问能否在犯错误概率不超过0.01的前提下，认为“移动支付活跃用户”与性别有关？

P(χ2≥k)	0.100	0.050	0.010
k	2.706	3.841	.635

	非移动支付活跃用户	移动支付活跃用户	合计
男
女
合计

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】有120粒试验种子需要播种，现有两种方案：方案一：将120粒种子分种在40个坑内，每坑3粒；方案二：120粒种子分种在60个坑内，每坑2粒如果每粒种子发芽的概率为0.5，并且，若一个坑内至少有1粒种子发芽，则这个坑不需要补种；若一个坑内的种子都没发芽，则这个坑需要补种（每个坑至多补种一次，且第二次补种的种子颗粒同第一次）.假定每个坑第一次播种需要2元，补种1个坑需1元；每个成活的坑可收货100粒试验种子，每粒试验种子收益1元.

(1)用表示播种费用，分别求出两种方案的的数学期望；